SOUSIC

哈库呐玛塔塔

0%

光流鲁棒性评估

发表于 更新于 分类于 ， Valine：
本文字数： 3.9k 阅读时长 ≈ 4 分钟
  1. 本篇文档对鲁棒性的定义：$$goodPoints/allPoints$$ 其中
  2. goodPoints：跟踪成功的特征点。即，向前-向后追踪回到开始帧，EPE 小于设定的阈值(单位: pixel)。
  3. allPoints：所有特征点
  4. 使用全部特征点测试鲁棒性，$$Harris \gtrsim Tomasi > Fast$$
  5. 使用我们的均匀化策略后的特征点测试鲁棒性，$$Fast > Tomasi \approx Harris$$

光流评估指标

误差指标

  • EPE(Endpoint Error)：估计光流和 ground-truth 光流的欧氏距离
    $$EPE = \sqrt{(u_{est} - u_{gt})^2 + (v_{est} - v_{gt})^2}$$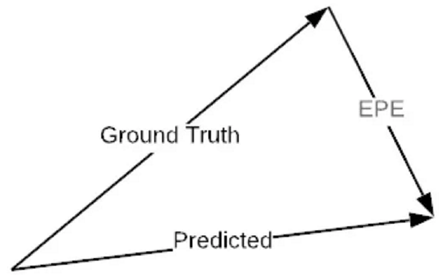
    EPE.png

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    std::vector<float> EndPointError(const std::vector<cv::Point2f>& prevPoints, const std::vector<cv::Point2f>& nextPoints, std::vector<uchar> status)
    {
        std::vector<float> endPointError;
        for (int i = 0; i < prevPoints.size(); i++)
        {
          const cv::Point2f prevP = prevPoints[i];
          const cv::Point2f nextP = nextPoints[i];
          float distance = 100.0;
          if ((bool)status[i])
          {
            const cv::Point2f diff = nextP - prevP;
            distance = sqrt((float)diff.ddot(diff));
          }
          endPointError.push_back(distance);
        }
        return endPointError;
    }

  • AE(Angular Error)：光流向量之间的角度误差。计算角度误差时增加一维，使用的是三维向量 (u, v, 1)
    $$\mathrm{AE}=\arccos \left(\frac{\left(\mathrm{u}{\mathrm{est}}, \mathrm{v}{\text {est }}, 1\right)^{\mathrm{T}} *\left(\mathrm{u}{\mathrm{gt}}, \mathrm{v}{\mathrm{gt}}, 1\right)}{\left.\sqrt{1.0+\mathrm{u}{\mathrm{est}} * \mathrm{u}{\mathrm{est}}+\mathrm{v}{\mathrm{est}} * \mathrm{v}{\mathrm{est}}} \sqrt{1.0+\mathrm{u}{\mathrm{gt}} * \mathrm{u}{\mathrm{gt}}+\mathrm{v}{\mathrm{gt}} * \mathrm{v}{\mathrm{gt}}}\right)}\right)$$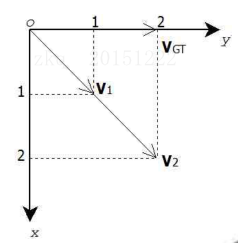
    AE.png

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    std::vector<float> AngularError(const std::vector<cv::Point2f>& prevPoints, const std::vector<cv::Point2f>& nextPoints, std::vector<uchar> status)
    {
        std::vector<float> angularErrs;
        for (int i = 0; i < prevPoints.size(); i++)
        {
          const cv::Point2f prevPoint2d = prevPoints[i];
          const cv::Point2f nextPoint2d = nextPoints[i];
          const cv::Point3f prevPoint3d(prevPoint2d.x, prevPoint2d.y, 1);
          const cv::Point3f nextPoint3d(nextPoint2d.x, nextPoint2d.y, 1);
          double angularErr = 100.0;
          if ((bool)status[i])
          {
            double vecDocVec = prevPoint3d.ddot(nextPoint3d);
            double vecNormProvecNorm = norm(prevPoint3d) * norm(nextPoint3d);
            double mid = vecDocVec / vecNormProvecNorm;
            double AE = acos(mid);
            angularErr = acos((double)(prevPoint3d.ddot(nextPoint3d) / norm(prevPoint3d) * norm(nextPoint3d)));
          }
          angularErrs.push_back(angularErr);
        }
        return angularErrs;
    }

统计指标

  • AEE：平均点误差
  • AAE：平均角误差

Datasets

MPI Sintel

从人工生成的动画 sintel 中得到光流 ground truth，每一个版本都包含 1041 个可用来训练的图片对，提供的 ground truth 十分密集，大幅度、小幅度的运动都包含。

sintel 数据集包括两种版本：

  • sintel final：包括运动模糊和一些环境氛围特效，如雾等
  • sintel clean：没有 final 的特效

Crowd-Flow

  • 序列包含 371 到 1451 个独立运动的个体
  • 数据集由 10 个长度范围的序列组成，在 300 至 450 帧之间，所有序列均以 25hz 的帧速率和高清分辨率呈现
  • 与此前光流数据集相比，该数据集除了提高了分辨率和帧的数量之外，还以连续序列而不是单帧对进行组织，允许评估时间一致性，例如以轨迹的形式

KITTI

只有一种特殊的动作类型（类似行车记录仪），并且位移很大，视频使用一个摄像头，ground-truth 由 3D 激光雷达得出，远距离的物体，如天空没法被捕捉，导致该数据集光流 ground-truth 比较稀疏。

  • KITTI 2012：194 组图片
  • KITTI 2015：200 组图片

Flying Chairs

软件渲染生成的虚拟数据，包含了 22872 对图像。

SceneFlow

利用软件渲染生成的虚拟立体数据集，包含 35454 个训练图像（有 ground truth），所有的图片分辨率都是 960x540。
主要包含三个子集：

  • FlyingThings3D
  • Driving
  • Monkaa

Middlebury

  • 评估使用 1.1 中的 4 个指标
  • gray 和 color 都有
  • 位移很小，通常小于10个像素
  • 12 个场景的图片流，每个场景图片只有 10 张
  • 针对的是全图片的光流，ground-truth 只有 1 帧的。需要把跑出来的光流结果保存成指定的数据格式(.flo)，上传到指定地址

数据集生成工具

  • AirSim：能够生成无人机视角和公路驾驶视角的两类数据
  • Carla：高仿真的自动驾驶场景

不依赖数据集评估方案

forward-backward

使用基于奇偶数的 forward-backward：如有 5 幅图像。前向时为 0-2-4，后向时为 4-3-1-0，连起来为 0-2-4-3-1-0。
最后使用欧氏距离计算出 0 帧与最后的 0 帧图像之间，特征点位置的漂移 e，即 final drift。设定一个阈值 threshold，计算小于 thresh 的特征点的百分比，为鲁棒性；e 的直方图用于表示稳定性。

1
2
3
4
5
6
7
8
9
10
11
12
13
float OpticalFlowRubost(std::vector<float> endpointErr, float thresh)
{
    int goodPoint = 0;
    int totalPoint = endpointErr.size();
    for (size_t i = 0; i < totalPoint; i++)
    {
      if (endpointErr[i] < thresh)
      {
        goodPoint++;
      }
    }
    return (float)goodPoint / (float)totalPoint;
}

Ref.