光流法
光流法是利用图像序列中的像素强度数据的时域变化和相关性来确定各自像素位置的“运动”。简单说来说,光流法的目的是找到灰度图中各像素在连续图像中的移动方向和速度。
光流法的实现要求满足几个基本假设:
- 相邻帧之间的亮度恒定;
- 相邻视频帧的取帧时间连续,或者,相邻帧之间物体的运动比较“微小”;
- 保持空间一致性;即,同一子图像的像素点具有相同的运动。
光流法的分类
基于梯度(微分法)
Horn-Schunck光流法
Horn-Schunck光流法基于全局平滑假设,即运动物体内部的光流场是相同的,因此物体内部光流场的梯度应该为零,也就是说物体内部的光流场应当是平滑的,故得到一个二阶梯度为0的约束方程。
特点:稠密光流,二阶导,计算量大
论文:Horn B K P, Schunck B G. Determining optical flow[J]. Artificial intelligence, 1981, 17(1-3): 185-203
Lucas-Kanade光流法
Lucas-Kanade算法认为:一个像素周围的相邻像素的光流场应该和中心的像素光流场一致。因此可以得到一系列等式,可以用最小二乘法求解。
特点:稀疏光流
论文:Baker S, Matthews I. Lucas-kanade 20 years on: A unifying framework[J]. International journal of computer vision, 2004, 56(3): 221-255.
基于图像金字塔的Lucas-Kanade光流法
普通的光流算法有一个问题——孔径问题。
同时,LK算法的约束条件——小速度,亮度不变以及区域一致性——都是较强的假设,并不很容易得到满足。如当物体运动速度较快时,假设不成立,那么后续的假设就会有较大的偏差,使得最终求出的光流值有较大的误差。
图像金字塔可以解决这个问题。
特点:稀疏光流
论文:Pyramidal Implementation of the Lucas Kanade Feature TrackerDescription of the algorithm
基于块匹配
先找出原图中的特征点,再在待匹配的图中的同一个位置附近区域使用块匹配的方法寻找最匹配的块。
块匹配的主要方法:
- SAD(绝对误差和)
- MAD(平均绝对差)
- SSD(误差平方和)
- MSD(平均误差平方和)
OpenCV中的光流法函数
具体API可以查看OpenCV官方文档
CalcOpticalFlowHS
HS光流法的实现
calcOpticalFlowPyrLK
基于图像金字塔的Lucas-Kanade光流法的实现
CalcOpticalFlowBM
通过块匹配的方法来计算光流
calcOpticalFlowFarneback
用Gunnar Farneback 的算法计算稠密光流(即图像上所有像素点的光流都计算出来)。
论文:Two-Frame Motion Estimation Based on PolynomialExpansion
calcOpticalFlowSF
论文:SimpleFlow: A Non-iterative, Sublinear Optical FlowAlgorithm
px4flow源码笔记
只用图像信息
c代码:去掉角速度,用随机生成的二维矩阵测试
compute_flow函数
参数
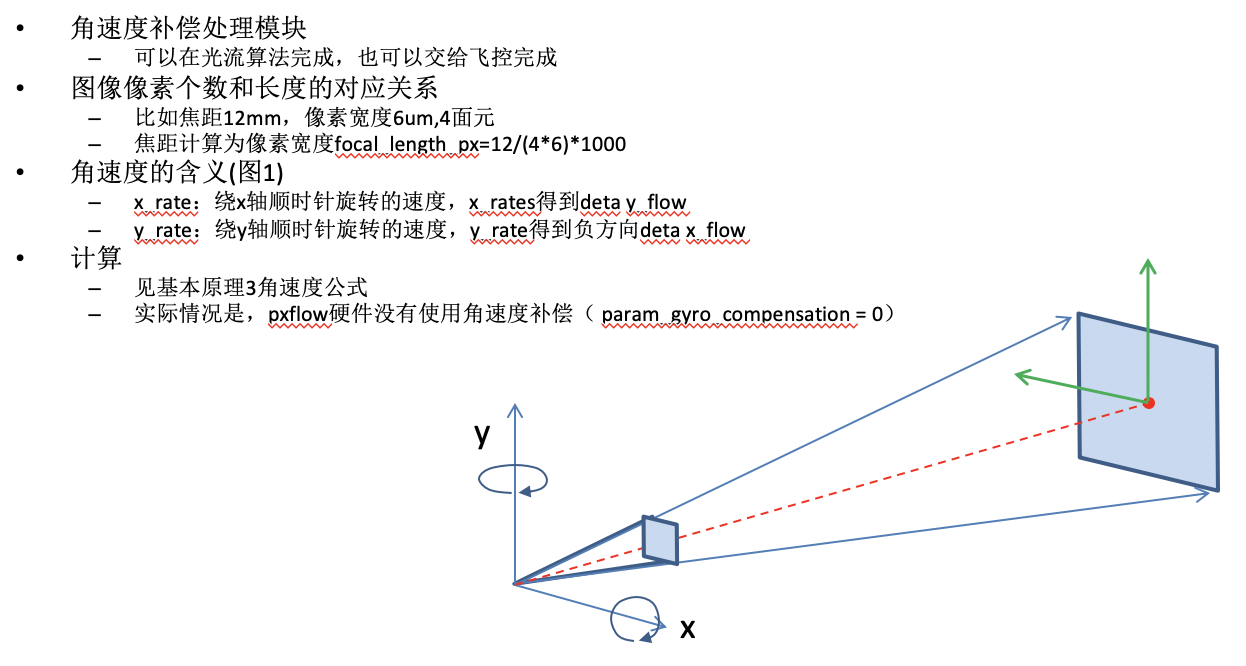
参数:*image1,*image2,x_rate,y_rate,z_rate,*pixel_flow_x, *pixel_flow_y
意义:图像1,图像2,绕x轴旋旋转速度,绕y轴旋转速度,绕z轴旋转速度,x轴像素移动,y轴像素移动
加了备注
函数伪码:
点击查看伪码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
def compute_flow():
for block_mid_pix in img1://步长为block的大小
diff = compute_diff()
if(diff<THRESHOLD): continue
for pix_in_win in img2:
temp_dist = ABSDIFF()
if(temp_dist<dist):
sumx = x偏移量
sumy = y偏移量
dist = temp_dist
if(dist<MIN_SAD):
meanflowx += sumx
meanflowy += sumy
compute_subpixel();//计算半像素
得到具有最小SAD的半像素方向mindir
dirsx[meancount] = sumx
dirsy[meancount] = sumy
subdirs[meancount] = mindir
meancount++
统计4个方向(类似坐标系的4个象限)的直方图
if(meancount>10)://特征点超过10个点
meanflowx /= meancount
meanflowy /= meancount
从直方图中找到4个方向中出现最多的方向
if(滤波):
滤波法
else:
平均法
//NUM_BLOCKS是一个维度被分成了几块
计算qual=meancount * 255 / (NUM_BLOCKS*NUM_BLOCKS)
分析
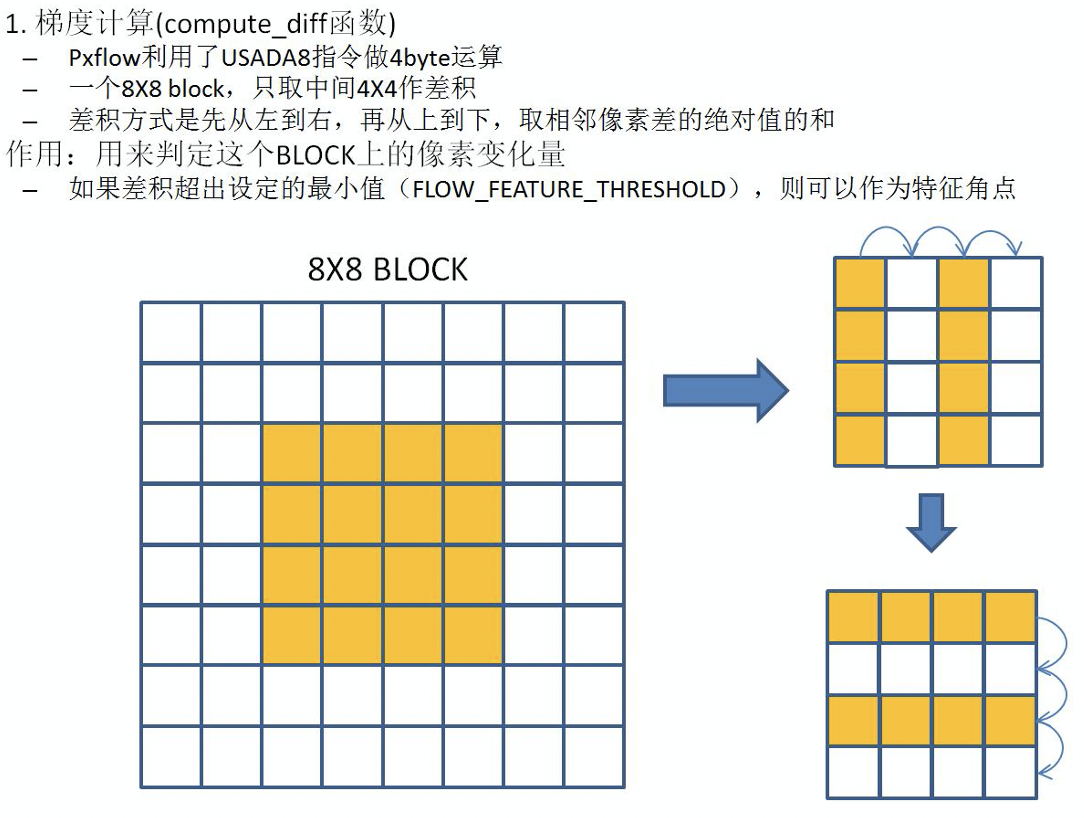
计算特征点使用了compute_diff函数,计算光流用的是SAD块匹配。
compute_diff(*image, offX, offY, row_size)
参数:图像,图像左上角像素的x坐标,图像左上角像素的y坐标
compute_subpixelcompute_subpixel(*image1,*image2,off1X,off1Y,off2X, off2Y,*acc,row_size)
参数:图像1,图像2,图像1左上角像素的x坐标,图像1左上角像素的y坐标,图像2左上角像素的x坐标,图像2左上角像素的y坐标,
计算流程
- 重要参数含义
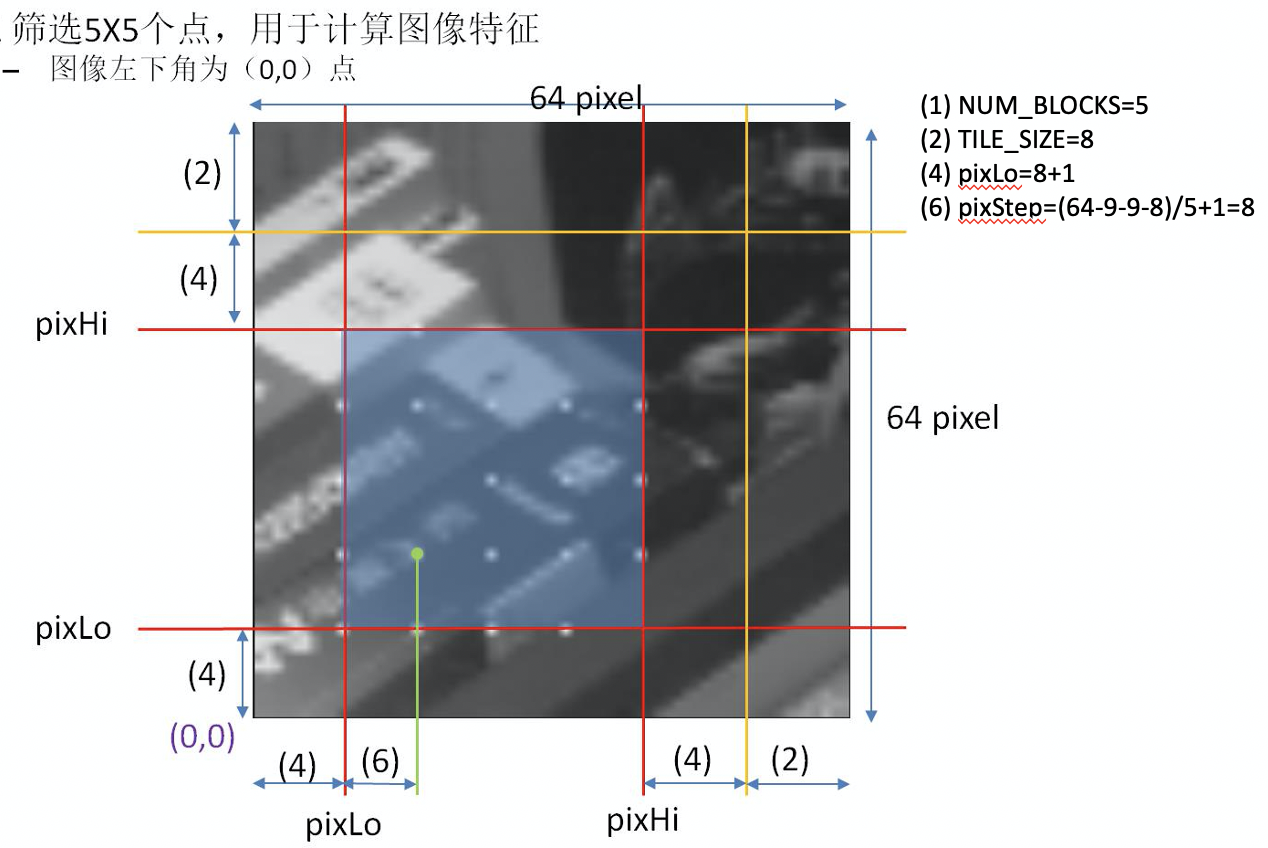
- 筛选特征点
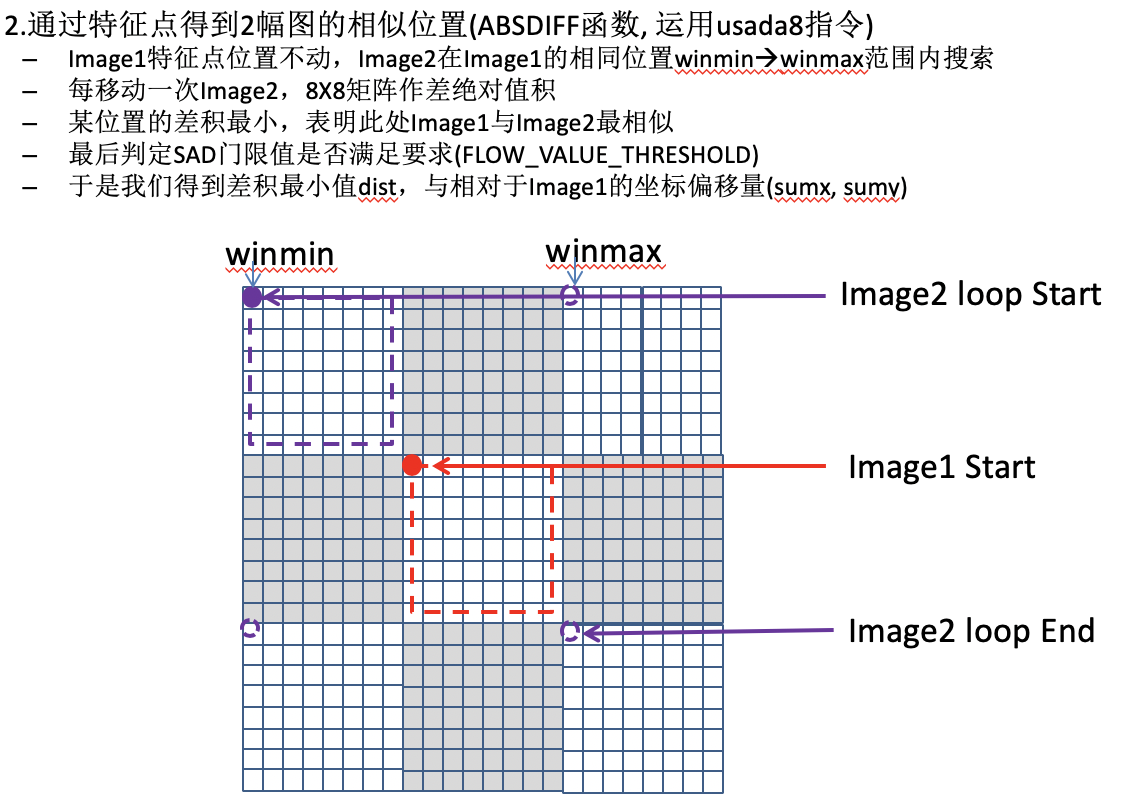
- 在附近搜索“距离”最近的块
- 半像素增加精度

- 直方图统计
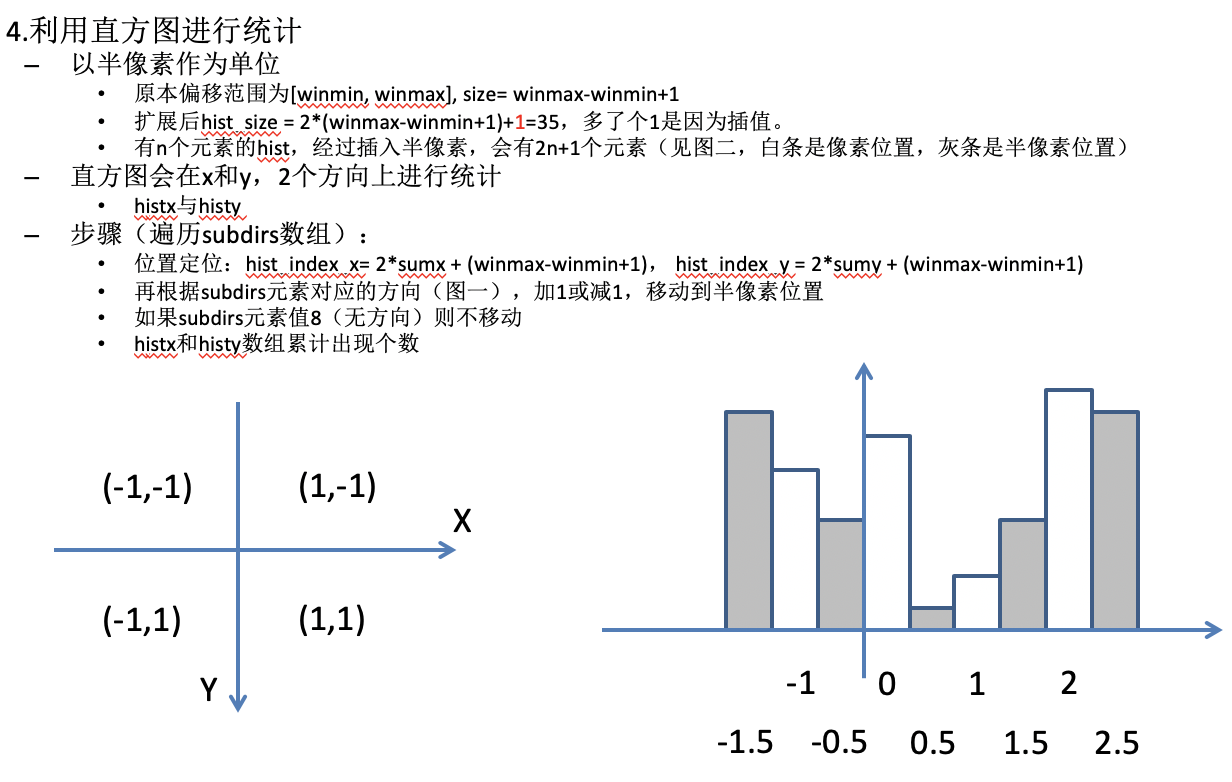
- 进一步计算:直方图法用统计数量峰值的前后两个像素数据(共5个)来取平均;平均法全部加起来取平均。

- 角速度补偿