SOUSIC

哈库呐玛塔塔

0%

SOUSIC的algorithm总结

发表于 更新于 分类于 Valine：
本文字数： 138k 阅读时长 ≈ 2:05

一、算法基础

大部分是Leecode中的典型题目，也有笔试中的真题和剑指Offer中的题目。题解使用C++，代码均由本人在参考题解之后所写。
相关github

1.1 常用数据结构

1.1.1 链表

链表又分为单链表（线性链表）、双向链表、循环链表

1.1.2 栈和队列

栈：后进先出（last-in,first-out,LIFO）
队列：先进先出（first-in,first-out,FIFO）
双端队列：一种特殊的队列，两端都可以进出

1.1.3 二叉树

是树型结构的一种特殊形式。二叉树中，刷题中用到的有

  • 二叉搜索树/二叉查找树，即左子树中的结点都比父结点小，右子树中的结点都比父结点大。
  • 平衡树二叉树（AVL树），就是在二叉树的基础上，若树中每棵子树都满足其左子树和右子树的深度差都不超过 1，则这棵二叉树就是平衡二叉树。

按照访问结点顺序的不同，可以将二叉树的遍历分为 前序遍历、中序遍历、后序遍历。

1.1.4 图

图是由顶点和边构成的数据结构，一般来说，顶点表示的是数据，边表示数据之间的联系。图可以简单的分为有向图和无向图。
可以用二维数组来存储一个图。

1.1.5 堆

  • 大根堆
  • 小根堆

1.2 时间复杂度、空间复杂度

算法中基本操作重复执行的次数是问题规模n的某个函数f(n)，把算法的执行时间记为T(n)=O(f(n))，他们的增长率相同，称做算法的渐进时间复杂度，简称时间复杂度。
相似的，空间复杂度S(n)=O(f(n))用来度量算法所需的存储空间。

1.3 排序（Sorting）、查找/搜索（Search）

1.3.1 排序

常用的八大排序：

  • 插入排序
  • 希尔排序
  • 选择排序
  • 冒泡排序
  • 快速排序
  • 堆排序
  • 归并排序
  • 基数排序

排序复杂度

1.3.2 查找/搜索

顺序查找：一般情况下步长为1。根据不同的要求，会设置不同的步长。时间复杂度为O(n)。
二分查找（Binary Search，又叫折半查找）：每次都与一个中点 mid = (low+hight)/2 相比较，时间复杂度为O(logn)。
二叉搜索/查找树：见1.1.3。中序遍历二叉搜索树可以有序的输出关键字。
树的遍历：前序遍历（根、左、右）、中序遍历（左、根、右）、后序遍历（左、右、根）。
广度优先搜索（BFS）：类似于树的层序遍历，先访问最近一层所有的结点，再访问下一层的。
深度优先（DFS）：类似于树的先序遍历，直到没有下一个结点才返回父结点。

1.4 递归

简单来说，递归的基本思想就是自己调用自己，这样就把问题变成了更小的子问题。
需要注意的是，递归函数中需要设置一个终止条件，以保证子问题最小时不再往下递归。

1.5 分治

分治策略中，需要递归的求解一个问题，在每层递归中会用到三个步骤[算法导论]：

  • 分解(Divide)：将原问题划分为规模更小的子问题。
  • 解决(Conquer)：递归的求解子问题。如果子问题足够小，停止递归直接求解。
  • 合并(Combine)：将子问题的解合成原问题的解。

二、数据结构类例题

主要从Leetcode的题中选出的代表性例题，也包括笔试或者其他资料上看到的比较好的题目。解答使用的cpp。

2.1 栈

单调栈

1. 739. 每日温度（中等）

根据每日 气温 列表，请重新生成一个列表，对应位置的输出是需要再等待多久温度才会升高超过该日的天数。如果之后都不会升高，请在该位置用 0 来代替。
例如，给定一个列表 temperatures = [73, 74, 75, 71, 69, 72, 76, 73]，你的输出应该是 [1, 1, 4, 2, 1, 1, 0, 0]。

提示：

1
气温 列表长度的范围是 [1, 30000]。每个气温的值的均为华氏度，都是在 [30, 100] 范围内的整数。

题解：
维护一个单调递减的栈，栈中元素为温度值的索引。当前温度比栈顶索引温度低时，直接进栈；当前温度比栈顶索引温度高时，两个索引之间的差就是栈顶索引值所求结果。
视频讲解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
vector<int> dailyTemperatures(vector<int>& T) {
    int n = T.size();
    vector<int> res(n,0);
    stack<int> s;
    for (int i = 0; i < n; ++i) {
        while (!s.empty() && T[i] > T[s.top()]) {
            int previousIndex = s.top();
            res[previousIndex] = i - previousIndex;
            s.pop();
        }
        s.push(i);
    }
    return res;
}

时间复杂度O(n)。空间复杂度O(n)。

两个栈实现队列

剑指 Offer 09. 用两个栈实现队列

用两个栈实现一个队列。队列的声明如下，请实现它的两个函数 appendTail 和 deleteHead ，分别完成在队列尾部插入整数和在队列头部删除整数的功能。(若队列中没有元素，deleteHead 操作返回 -1 )

示例 1：

1
2
3
4
输入：
["CQueue","appendTail","deleteHead","deleteHead"]
[[],[3],[],[]]
输出：[null,null,3,-1]

题解：
一个栈入，一个栈出。当要插入数据时，直接插入入栈；当要取出数据时，如果出栈不为空，则从入栈依次取出放入出栈，直到入栈为空。这样就能保证后进先出。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class CQueue {
    stack<int> inputStack, outputStack;
public:
    CQueue() {
        while(!inputStack.empty())
            inputStack.pop();
        while(!outputStack.empty())
            outputStack.pop();
    }
    
    void appendTail(int value) {
        inputStack.push(value);
    }
    
    int deleteHead() {
        if(outputStack.empty()){
            while(!inputStack.empty()){
                outputStack.push(inputStack.top());
                inputStack.pop();
            }
        }
        if(outputStack.empty())
            return -1;
        else{
            int output = outputStack.top();
            outputStack.pop();
            return output;
        }
    }
};

栈排序

使用两个栈进行排序（或着说使用一个辅助栈对栈进行排序）

每次都往辅助栈中放如当前剩余的最大的值，最后直到当前栈空了，再把辅助栈转移回去就可以完成排序。

弹出一个数：

  • 辅助栈为空，push
  • 辅助栈不为空，如果弹出值大于辅助栈顶，则弹出辅助栈的元素放入当前栈，直到遇到小于或等于的就push进辅助栈。
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    //栈顶最大
    void sortStackByStack(stack<int> &st){
        stack<int> help;
        while(!st.empty()){
            int curr=st.top();
            st.pop();
            while(!help.empty() && curr>help.top() ){
                st.push(help.top());
                help.pop();
            }
            help.push(curr);
        }
        while(!help.empty()){
            int tmp=help.top();
            help.pop();
            st.push(tmp);
        }
    }

2.2 二叉树

二叉树的遍历

二叉树的遍历可以实现很多树相关的操作，如二叉树的序列化。二叉树的序列化本质上是对其值进行编码，更重要的是对其结构进行编码。可以遍历树来完成。

二叉树遍历的cpp实现

我们一般有两个策略：

BFS（即层序遍历）：BFS 可以按照层次的顺序从上到下遍历所有的节点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
void levelOrder(BinaryTree *root){
    queue<BinaryTree *> que;
    que.push(root);

    while(!que.empty()){
        BinaryTree *curNode = que.front();
        cout << curNode->val << " ";
        que.pop();
        if(curNode->lc!=nullptr)
            que.push(curNode->lc);
        if(curNode->rc!=nullptr)
            que.push(curNode->rc);
    }
}

DFS：DFS 可以从一个根开始，一直延伸到某个叶，然后回到根，到达另一个分支。根据根节点、左节点和右节点之间的相对顺序，可以进一步将DFS策略区分为：

先序遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
//递归
void preOrder_recursion(BinaryTree *root){
    if(root==nullptr)
        return;
    cout << root->val << " ";
    preOrder_recursion(root->lc);
    preOrder_recursion(root->rc);
}

//非递归
void preOrder_non_recursion(BinaryTree *root){
    stack<BinaryTree *> st;

    while(root!=nullptr || !st.empty()){
        if(root!=nullptr){
            cout << root->val << " ";
            st.push(root);
            root = root->lc;
        }else{
            root = st.top();
            st.pop();
            root = root->rc;
        }
    }
}
中序遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
//递归
void inOrder_recursion(BinaryTree *root){
    if(root==nullptr)
        return;
    inOrder_recursion(root->lc);
    cout << root->val << " ";
    inOrder_recursion(root->rc);
}

//非递归
void inOrder_non_recursion(BinaryTree *root){
    stack<BinaryTree *> st;

    while(root!=nullptr || !st.empty()){
        if(root!=nullptr){
            st.push(root);
            root = root->lc;
        }else{
            root = st.top();
            st.pop();
            cout << root->val << " ";
            root = root->rc;
        }
    }
}
后序遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
//递归
void posOrder_recursion(BinaryTree *root){
    if(root==nullptr)
        return;
    posOrder_recursion(root->lc);
    posOrder_recursion(root->rc);
    cout << root->val << " ";
}

//非递归
void posOrder_non_recursion(BinaryTree *root){
    stack<BinaryTree *> st;
    BinaryTree *lastVisited = root;

    while(root!=nullptr || !st.empty()){
        if(root!=nullptr){
            st.push(root);
            root = root->lc;
        }else{
            root = st.top();
            if(root->lc == nullptr || root->rc == lastVisited){
                cout << root->val << " ";
                st.pop();
                lastVisited = root;
                root = nullptr;
            }else{
                root = root->rc;
            }
        }
    }
}

Z形遍历/锯齿形遍历

Leetcode 103. 二叉树的锯齿形层次遍历（中等）
在层序遍历的基础上加了一个reverse标记，reverse为true时反向遍历。由于头和尾都要插入和弹出，使用双端队列deque会好一些，使用vector的insert比较耗时。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
vector<vector<int>> zigzagLevelOrder(TreeNode* root) {
    if(root==nullptr)
        return {};
    vector<vector<int> > res;
    deque<TreeNode *> dque;
    dque.push_back(root);
    bool reverse = false;
    while(!dque.empty()){
        int n = dque.size();
        vector<int> tmp;
        TreeNode *cur;
        while(n--){
            if(reverse){//后取前放
                cur = dque.back();
                dque.pop_back();
                if(cur->right) dque.push_front(cur->right);//先右再左
                if(cur->left) dque.push_front(cur->left);
            }else{//前取后放
                cur = dque.front();
                dque.pop_front();
                if(cur->left) dque.push_back(cur->left);//先左再右
                if(cur->right) dque.push_back(cur->right);
            }
            tmp.push_back(cur->val);
        }
        res.push_back(tmp);
        reverse = !reverse;
    }
    return res;
}

时间复杂度：O(n)
空间复杂度：O(n)

1. 1028. 从先序遍历还原二叉树（困难）

我们从二叉树的根节点 root 开始进行深度优先搜索。
在遍历中的每个节点处，我们输出 D 条短划线（其中 D 是该节点的深度），然后输出该节点的值。（如果节点的深度为 D，则其直接子节点的深度为 D + 1。根节点的深度为 0）。
如果节点只有一个子节点，那么保证该子节点为左子节点。
给出遍历输出 S，还原树并返回其根节点 root。

示例1:

1
2
输入："1-2--3--4-5--6--7"
输出：[1,2,5,3,4,6,7]

示例2:

1
2
输入："1-2--3---4-5--6---7"
输出：[1,2,5,3,null,6,null,4,null,7]

示例 3：

1
2
输入："1-401--349---90--88"
输出：[1,401,null,349,88,90]

题解：
当前节点为T，上一个节点为S，只有两种情况：

  • T 是 S 的左子节点；
  • T 是根节点到 S 这一条路径上（不包括 S，因为题目中规定了如果节点只有一个子节点，那么保证该子节点为左子节点）某一个节点的右子节点。

所以，我们用一个栈保存根节点到当前节点的上一个节点的路径：

  1. 当前节点的深度刚好比栈的高度大1：当前节点正好是栈顶节点的左子节点；ps. 深度是从0开始，所以当深度的值和栈高度相等时，就是深度刚好比栈的高度大1
  2. 当前节点的深度小于等于栈的高度：
    • 当前节点的深度刚和栈的高度相等：当前节点是栈顶节点右兄弟节点即栈顶节点父节点的右子节点；
    • 当前节点的深度小于栈的高度：当前节点是根节点到栈顶节点路径上某一个节点的右子节点。一直弹出栈顶节点直到满足情况1。
    • *ps. 当前节点的深度刚和栈的高度相等 即 level=path.size()-1，也是需要弹出栈顶节点一次*
      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      15
      16
      17
      18
      19
      20
      21
      22
      23
      24
      25
      26
      27
      28
      29
      30
      31
      TreeNode* recoverFromPreorder(string S) {
          stack<TreeNode *> path;
          int pos = 0;
          while(pos<S.size()){
              int level = 0;
              while(S[pos]=='-'){
                  level++;
                  pos++;
              }
              
              int value = 0;
              while (pos < S.size() && isdigit(S[pos])){//取当前节点的值
                  value = value * 10 + (S[pos] - '0');
                  pos++;
              }

              TreeNode *node = new TreeNode(value);
              if(level==path.size()){//第1种情况
                  if(!path.empty())
                      path.top()->left = node;
              }else{//第2种情况
                  while(level!=path.size())
                      path.pop();
                  path.top()->right = node;
              }
              path.push(node);
          }
          while(path.size()>1)
              path.pop();
          return path.top();
      }
      时间复杂度：O(n)。n为S的长度
      空间复杂度：O(h)。h为树的高度

2. 104. 二叉树的最大深度（简单）

给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明: 叶子节点是指没有子节点的节点。

示例：

1
2
3
4
5
6
7
给定二叉树 [3,9,20,null,null,15,7]，
    3
   / \
  9  20
    /  \
   15   7
返回它的最大深度 3 。

题解：

  1. 层序遍历（BFS）。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    int maxDepth(TreeNode* root){
        if(root==nullptr)
            return 0;
        queue<TreeNode*> que;
        que.push(root);
        int hight = 0;
        while(!que.empty()){
            hight++;
            int n = que.size();
            for (int i = 0; i < n; i++)
            {
                TreeNode *curNode = que.front();
                que.pop();
                if(curNode->left!=nullptr)
                    que.push(curNode->left);
                if(curNode->right!=nullptr)
                    que.push(curNode->right);
            }
        }
        return hight;
    }

    时间复杂度：O(n)
    空间复杂度：O(n)

  2. 递归。

    1
    2
    3
    4
    5
    int maxDepth(TreeNode* root){
        if(root==nullptr)
            return 0;
        return max(maxDepth(root->left), maxDepth(root->right)) + 1;
    }

    时间复杂度：O(n)
    空间复杂度：O(hight)

3. 110. 平衡二叉树（简单）

给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：
一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过1。

示例 1:

1
2
3
4
5
6
7
给定二叉树 [3,9,20,null,null,15,7]
    3
   / \
  9  20
    /  \
   15   7
返回 true 。

示例 2:

1
2
3
4
5
6
7
8
9
给定二叉树 [1,2,2,3,3,null,null,4,4]
       1
      / \
     2   2
    / \
   3   3
  / \
 4   4
返回 false 。

题解：
用到上一题的求深度。

  1. 自上而下递归。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    int getHight(TreeNode *root){
        if(root==nullptr)
            return 0;
        return max(getHight(root->left),getHight(root->right))+1;
    }

    bool isBalanced(TreeNode* root) {
        if(root==nullptr)
            return true;
        return abs(getHight(root->left)-getHight(root->right))<2 
                && isBalanced(root->left)
                && isBalanced(root->right);
    }

    时间复杂度：O(nlogn)
    空间复杂度：O(n)

  2. 自下而上递归。加了一个hight记录子树高度。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    bool helper(TreeNode *root, int &height){
        if(root==nullptr){
            height = -1;
            return true;
        }

        int left,right;
        if(helper(root->left,left) && helper(root->right,right) && abs(left-right)<2){
            height = max(left,right)+1;
            return true;
        }
        return false;
    }

    bool isBalanced(TreeNode* root) {
        int height;
        return helper(root,height);
    }

    时间复杂度：O(n)
    空间复杂度：O(n)

4. 530. 二叉搜索树的最小绝对差（简单）

给你一棵所有节点为非负值的二叉搜索树，请你计算树中任意两节点的差的绝对值的最小值。

示例：

1
2
3
4
5
6
7
8
9
10
11
12
13
输入：

   1
    \
     3
    /
   2

输出：
1

解释：
最小绝对差为 1，其中 2 和 1 的差的绝对值为 1（或者 2 和 3）。

题解：
搜索二叉树的中序遍历就是升序排列，所以中序遍历是记录上一个节点的值，就可以求差值，维护一个最小值可以一边遍历得到答案。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int res = INT_MAX;
void midOrder(TreeNode* root, int &last){ //注意last要用引用，不然弹栈的时候上一个节点的值不能被记录
    if(!root)
        return;
    midOrder(root->left, last);
    if(last==-1)
        last = root->val;
    else
        res = min(res, abs(root->val-last));
    last = root->val;
    midOrder(root->right, last);
}
int getMinimumDifference(TreeNode* root) {
    int last = -1;
    midOrder(root, last);
    return res;
}

时间复杂度：O(n)
空间复杂度：O(n)，搜索二叉树可以会退化成链

5. 剑指 Offer 68 - I. 二叉搜索树的最近公共祖先（简单）

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

示例：

1
2
3
4
5
6
7
8
9
10
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6 
解释: 节点 2 和节点 8 的最近公共祖先是 6。
    6
   / \
  2   8
 /\   /\
0  4 7  9
  /\
 3  5

题解：
要判断一个节点的左子树里有p，右子树里有q，那么当前节点就是最近公共祖先。从上往下遍历的时候，如果(p->val <= cur->val && cur->val <= q->val)则说明该节点cur就是最近公共祖先了。

1
2
3
4
5
6
7
8
9
10
11
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
    while(root){
        if(root->val > p->val && root->val > q->val)
            root = root->left;
        else if(root->val < p->val && root->val < q->val)
            root = root->right;
        else
            return root;
    }
    return nullptr;
}

时间复杂度：O(n)
空间复杂度：O(1)

6. 236. 二叉树的最近公共祖先（中等）

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先 Lowest Common Ancestor(LCA)。上一题是二叉搜索树。

示例：

1
2
3
4
5
6
7
8
9
10
11
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出: 3
解释: 节点 5 和节点 1 的最近公共祖先是节点 3。

    3
   / \
  5   1
 /\   /\
6  2 0  8
  /\
 7  4

题解：

  1. 递归。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
TreeNode* ans;
bool dfs(TreeNode* root, TreeNode* p, TreeNode* q) {
    if (root == nullptr) return false;
    bool lson = dfs(root->left, p, q);
    bool rson = dfs(root->right, p, q);
    if ((lson && rson) || ((root->val == p->val || root->val == q->val) && (lson || rson))){// (左右都包含p/q) || (一边子树包含另p/q + 一边root节点是p/q)
        ans = root;
    } 
    return lson || rson || (root->val == p->val || root->val == q->val); //左子树包含||右子树包含||root为p/q
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
    dfs(root, p, q);
    return ans;
}

时间复杂度：O(n)
空间复杂度：O(n)

  1. 可以用哈希表存储所有节点的父节点，然后就可以利用节点的父节点信息从 p 结点开始不断往上跳，并记录已经访问过的节点，再从 q 节点开始不断往上跳，如果碰到已经访问过的节点，那么这个节点就是我们要找的最近公共祖先。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
unordered_map<int, TreeNode*> parents;
unordered_map<int, bool> visited;
void dfs(TreeNode* root){//记录父节点
    if (root->left != nullptr) {
        parents[root->left->val] = root;
        dfs(root->left);
    }
    if (root->right != nullptr) {
        parents[root->right->val] = root;
        dfs(root->right);
    }
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
    parents[root->val] = nullptr;
    dfs(root);
    while (p != nullptr) {//从p往上走，也可以从q
        visited[p->val] = true;
        p = parents[p->val];
    }
    while (q != nullptr) {
        if (visited[q->val]) return q;
        q = parents[q->val];//从q往上走，碰到的第一个已经访问过的节点即为LCA节点
    }
    return nullptr;
}

时间复杂度：O(n)
空间复杂度：O(n)

2.3 链表

面试题 02.01. 移除重复节点（简单）

编写代码，移除未排序链表中的重复节点。保留最开始出现的节点。

示例1:

1
2
输入：[1, 2, 3, 3, 2, 1]
输出：[1, 2, 3]

示例2:

1
2
输入：[1, 1, 1, 1, 2]
输出：[1, 2]

题解：
用一个哈希表(unordered_set)保存已有元素。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
ListNode* removeDuplicateNodes(ListNode* head) {
    if(head==nullptr || head->next==nullptr)
        return head;

    unordered_set<int> valSet;
    ListNode *lastNode = head;
    ListNode *cur = head->next;
    valSet.insert(head->val);
    while (cur != nullptr)
    {
        if(valSet.find(cur->val) == valSet.end()){//非重复节点
            valSet.insert(cur->val);
            lastNode->next = cur;
            lastNode = lastNode->next;
            cur = cur->next;
        }else{//重复节点
            cur = cur->next;
        }
    }
    lastNode->next = cur;//nullptr

    return head;
}

时间复杂度：O(n)
空间复杂度：O(n)

ps. 在不允许用额外空间的情况下，可以用两重循环。时间O(n^2) ，空间o(1)。

206. 反转链表（简单）

反转一个单链表。

示例:

1
2
输入: 1->2->3->4->5->NULL
输出: 5->4->3->2->1->NULL

题解：

  1. 遍历反转。
1
2
3
4
5
6
7
8
9
10
11
12
13
ListNode* reverseList(ListNode* head) {
    if(head==nullptr || head->next==nullptr)
        return head;
    ListNode *pre = nullptr;
    ListNode *cur = head;
    while(cur!=nullptr){
        ListNode *tmp = cur->next;
        cur->next = pre;
        pre = cur;
        cur = tmp;
    }
    return pre;
}

时间复杂度：O(n)
空间复杂度：O(1)

  1. 递归。
1
2
3
4
5
6
7
8
ListNode* reverseList(ListNode* head) {
    if(head==nullptr || head->next==nullptr)
        return head;
    ListNode *cur = reverseList(head->next);
    head->next->next = head;
    head->next = nullptr;
    return cur;
}

时间复杂度：O(n)
空间复杂度：O(n)

25. K 个一组翻转链表（困难）

给你一个链表，每 k 个节点一组进行翻转，请你返回翻转后的链表。

k 是一个正整数，它的值小于或等于链表的长度。

如果节点总数不是 k 的整数倍，那么请将最后剩余的节点保持原有顺序。

示例：

1
2
3
4
5
给你这个链表：1->2->3->4->5

当 k = 2 时，应当返回: 2->1->4->3->5

当 k = 3 时，应当返回: 3->2->1->4->5

题解： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
pair<ListNode*, ListNode*> reverseList(ListNode* head, ListNode* rear){
    ListNode *pre = rear->next;
    ListNode *cur = head;
    while(pre != rear){
        ListNode *tmp = cur->next;
        cur->next = pre;
        pre = cur;
        cur = tmp;
    }
    return {rear, head};//非递归反转链表并返回新链表头尾
}

ListNode* reverseKGroup(ListNode* head, int k) {
	ListNode *res = new ListNode(0);
	res->next = head;
	ListNode *preNode = res, *L = head;
	ListNode *R, *nextNode;
	while(L){
		R = preNode;
		for (int i = 0; i < k; i++){  //选出要反转的k个
			R = R->next;
			if(R==nullptr)//剩下的不足k个直接返回
				return res->next;
		}
		nextNode = R->next;
		auto ret = reverseList(L, R);
		L = ret.first;
		R = ret.second;
        //把子链表重新接回原链表
		preNode->next = L;
		R->next = nextNode;
		preNode = R;
		L = R->next;
	}
	return res->next;
}

时间复杂度：O(n)
空间复杂度：O(1)

92. 反转链表 II（中等）

反转从位置 m 到 n 的链表。请使用一趟扫描完成反转。

说明:1 ≤ m ≤ n ≤ 链表长度。

示例:

1
2
输入: 1->2->3->4->5->NULL, m = 2, n = 4
输出: 1->4->3->2->5->NULL

题解：

  1. 遍历交换。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    ListNode* reverseBetween(ListNode* head, int m, int n) {
        if(m==n)
            return head;
        if(m==1){
            ListNode *lastRevers = head;
            ListNode *pre = lastRevers;
            ListNode *cur = pre->next;
            for(int i=m;i<n;i++){
                ListNode *tmp = cur->next;
                cur->next = pre;
                pre = cur;
                cur = tmp;
            }
            lastRevers->next = cur;
            return pre;
        }else{
            ListNode *before = head;
            for(int i=1;i<m-1;i++)
                before = before->next;
            ListNode *lastRevers = before->next;
            ListNode *pre = lastRevers;
            ListNode *cur = pre->next;
            for(int i=m;i<n;i++){
                ListNode *tmp = cur->next;
                cur->next = pre;
                pre = cur;
                cur = tmp;
            }
            before->next = pre;
            lastRevers->next = cur;
            return head;
        }
    }

    时间复杂度：O(n)
    空间复杂度：O(1)

  2. 头插法。双指针，一个指针 A 指向要反转的前一个节点m-1，一个指针 B 指向要反转的第一个节点m。B在往后移动时，不停的把B后面的一个节点移到A后面，一直到n-1结束。这时已经反转了要求的链表。
    ps. new一个节点指向头节点，就可以解决m=1的情况

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    ListNode* reverseBetween(ListNode* head, int m, int n) {
        ListNode *preHead = new ListNode(0);
        preHead->next = head;

        ListNode *A = preHead;
        ListNode *B = head;

        int step = 0;
        while (step < m - 1) {
            A = A->next; B = B->next;
            step++;
        }

        for (int i = 0; i < n - m; i++) {
            ListNode *removed = B->next;
            B->next = B->next->next;

            removed->next = A->next;
            A->next = removed;
        }

        return preHead->next;
    }

    时间复杂度：O(n)
    空间复杂度：O(1)

142. 环形链表 II（中等）

给定一个链表，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。 如果 pos 是 -1，则在该链表中没有环。

说明：不允许修改给定的链表。

示例 1：

1
2
3
输入：head = [3,2,0,-4], pos = 1
输出：tail connects to node index 1
解释：链表中有一个环，其尾部连接到第二个节点。

题解：

  1. 哈希表。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    ListNode *detectCycle(ListNode *head) {
        unordered_map<ListNode*,int> nodeMap;
        ListNode *cur = head;
        while(cur){
            if(++nodeMap[cur]>1)
                return cur;
            cur = cur->next;
        }
        return nullptr;
    }

    时间复杂度：O(n)
    空间复杂度：O(n)

  2. 快慢指针。
    快指针一次走2步，慢指针一次走一步。

  • 快指针走到nullptr，说明无环
  • 快指针慢指针第一次相遇节点记为mark，这时把慢指针移到头节点，快指针不变。他们都继续移动，都是一次走一步。当两个指针再次相遇时，就是头节点。
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    ListNode *detectCycle(ListNode *head) {
        if(head == nullptr || head->next == nullptr)
            return nullptr;
        ListNode *fast = head, *slow = head;
        do{
            if(fast == nullptr || fast->next == nullptr)
                return nullptr;
            fast = fast->next->next;
            slow = slow->next;
        }while(fast!=slow);

        slow = head;
        while(fast!=slow){
            fast = fast->next;
            slow = slow->next;
        }
        return fast;
    }
    时间复杂度：O(n)
    空间复杂度：O(1)

2.4 图

1. 5211. 概率最大的路径（中等）

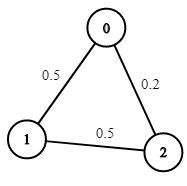
给你一个由 n 个节点（下标从 0 开始）组成的无向加权图，该图由一个描述边的列表组成，其中 edges[i] = [a, b] 表示连接节点 a 和 b 的一条无向边，且该边遍历成功的概率为 succProb[i] 。

指定两个节点分别作为起点 start 和终点 end ，请你找出从起点到终点成功概率最大的路径，并返回其成功概率。

如果不存在从 start 到 end 的路径，请 返回 0 。只要答案与标准答案的误差不超过 1e-5 ，就会被视作正确答案。

示例 1：
ex1

1
2
3
输入：n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.2], start = 0, end = 2
输出：0.25000
解释：从起点到终点有两条路径，其中一条的成功概率为 0.2 ，而另一条为 0.5 * 0.5 = 0.25

题解：

  • 先建图。graph[i] 表示第 i 个节点能够到达的下一个节点及概率。
  • bfs把与当前节点有连接的节点存入一个大根堆。（如果只用队列会出错）
  • hasVisited[i] 表示 i 节点是否被访问过
  • 循环直到堆为空

其实就是 Dijkstra 算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
const double zero = 1e-8;

vector<vector<pair<int,double> > > buildGrapg(vector<vector<int> > &edges, vector<double>& succProb, int n){
    vector<vector<pair<int,double> > > graph(n);
    for (int i = 0; i < edges.size();i++)
    {
        graph[edges[i][0]].emplace_back(edges[i][1],succProb[i]);
        graph[edges[i][1]].emplace_back(edges[i][0],succProb[i]);
    }
    return graph;
}

double maxProbability(int n, vector<vector<int> >& edges, vector<double>& succProb, int start, int end) {
    if(edges.empty())
        return 0.0;
    vector<vector<pair<int,double> > > graph = buildGrapg(edges, succProb, n);
    if(graph[end].empty() || graph[start].empty())
        return 0.0;

    vector<double> prob(n, 0.0); //从start到每个节点的最大概率
    prob[start] = 1;
    priority_queue<pair<double, int> > que;
    vector<bool> hasVisited(n， false);
    que.push({1, start});
    while(!que.empty()){
        auto cur = que.top();
        que.pop();
        double p = cur.first;
        int node = cur.second;
        if(hasVisited[node])
            continue;
        hasVisited[node] = true;
        if(p<zero)
            continue;
        for(auto edge:graph[node]){
            int v = edge.first;
            double curProb = p * edge.second;
            if(prob[v]<curProb){
                prob[v] = curProb;
                que.push({prob[v], v});
            }
        }
    }
    return prob[end];
}

2. 207. 课程表（中等）有向图的拓扑排序

你这个学期必须选修 numCourse 门课程，记为 0 到 numCourse-1 。

在选修某些课程之前需要一些先修课程。 例如，想要学习课程 0 ，你需要先完成课程 1 ，我们用一个匹配来表示他们：[0,1]

给定课程总量以及它们的先决条件，请你判断是否可能完成所有课程的学习？

示例 1:

1
2
3
输入: 2, [[1,0]] 
输出: true
解释: 总共有 2 门课程。学习课程 1 之前，你需要完成课程 0。所以这是可能的。

示例 2:

1
2
3
输入: 2, [[1,0],[0,1]]
输出: false
解释: 总共有 2 门课程。学习课程 1 之前，你需要先完成​课程 0；并且学习课程 0 之前，你还应先完成课程 1。这是不可能的。

提示：

1
2
3
输入的先决条件是由 边缘列表 表示的图形，而不是 邻接矩阵 。详情请参见图的表示法。
你可以假定输入的先决条件中没有重复的边。
1 <= numCourses <= 10^5

题解：

  1. 有向图的dfs遍历。
    visited[i]表示第i和节点的状态，0表示没有被访问过，1表示正在被访问，2表示访问结束的节点。circle表示有向图有环。使用dfs遍历有向图：
  • 当正在访问的节点（visited[i]=1）又被访问时，说明有向图存在环，返回false。
  • 全部节点访问完毕，返回true
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    bool circle = false;

    void dfs(int u, vector<vector<int> > &graph, vector<int> &visited){
        visited[u] = 1;//正在访问该节点
        for(int v:graph[u]){
            if(visited[v]==0){
                dfs(v, graph, visited);
                if(circle)
                    return;
            }else if(visited[v]==1){
                circle = true;
                return;
            }
        }
        visited[u] = 2;
    }

    bool canFinish(int numCourses, vector<vector<int> >& prerequisites) {
        if(prerequisites.empty())
            return true;
        vector<vector<int> > graph(numCourses);
        for (auto course : prerequisites)
        {//build graph
            graph[course[1]].push_back(course[0]);
        }

        vector<int> visited(numCourses);
        for (int i = 0; i < numCourses && !circle; i++)
        {
            if(!visited[i])
                dfs(i, graph, visited);
        }
        return !circle;
    }
    时间复杂度：O(m+n)。m是有向图的边，n是有向图的节点。
    空间复杂度：O(m+n)
  1. bfs入度为0的点
    拓扑排序中，起点都是入度为0的点。把所有入度为0的节点放入队列，依次访问队列中的节点。访问的时候把所有从该节点出去的边都删掉，即该节点出发连接的边的入度都减1。再把入度减到0的点加入队列。
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    bool canFinish(int numCourses, vector<vector<int> >& prerequisites) {
        if(prerequisites.empty())
            return true;
        vector<vector<int> > graph(numCourses);
        vector<int> inDegree(numCourses, 0);
        for (auto course : prerequisites)
        {//build graph
            graph[course[1]].push_back(course[0]);
            inDegree[course[0]]++;
        }

        queue<int> que;
        for (int i = 0; i < numCourses;i++)
        {
            if(inDegree[i]==0)
                que.push(i);
        }

        int visited = 0;
        while (!que.empty())
        {
            visited++;
            int u = que.front();
            que.pop();
            for(int v:graph[u]){
                inDegree[v]--;
                if(inDegree[v]==0)
                    que.push(v);
            }
        }
        return visited == numCourses;
    }
    时间复杂度：O(m+n)。m是有向图的边，n是有向图的节点。
    空间复杂度：O(m+n)

3.210. 课程表 II（中等）

现在你总共有 n 门课需要选，记为 0 到 n-1。

在选修某些课程之前需要一些先修课程。 例如，想要学习课程 0 ，你需要先完成课程 1 ，我们用一个匹配来表示他们: [0,1]

给定课程总量以及它们的先决条件，返回你为了学完所有课程所安排的学习顺序。

可能会有多个正确的顺序，你只要返回一种就可以了。如果不可能完成所有课程，返回一个空数组。

示例 1:

1
2
3
输入: 2, [[1,0]] 
输出: [0,1]
解释: 总共有 2 门课程。要学习课程 1，你需要先完成课程 0。因此，正确的课程顺序为 [0,1] 。

示例 2:

1
2
3
4
输入: 4, [[1,0],[2,0],[3,1],[3,2]]
输出: [0,1,2,3] or [0,2,1,3]
解释: 总共有 4 门课程。要学习课程 3，你应该先完成课程 1 和课程 2。并且课程 1 和课程 2 都应该排在课程 0 之后。
     因此，一个正确的课程顺序是 [0,1,2,3] 。另一个正确的排序是 [0,2,1,3] 。

说明:

1
2
输入的先决条件是由边缘列表表示的图形，而不是邻接矩阵。详情请参见图的表示法。
你可以假定输入的先决条件中没有重复的边。

提示:

1
2
3
这个问题相当于查找一个循环是否存在于有向图中。如果存在循环，则不存在拓扑排序，因此不可能选取所有课程进行学习。
通过 DFS 进行拓扑排序 - 一个关于Coursera的精彩视频教程（21分钟），介绍拓扑排序的基本概念。
拓扑排序也可以通过 BFS 完成。

题解：

  1. dfs。和上一题基本相同，只需要在节点访问完成时放入结果向量，因为dfs先访问的是最后的节点，所以需要把向量反转一下。
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    bool circle = false;
    vector<int> res;

    void dfs(int u, vector<vector<int> > &graph, vector<int> &visited){
        visited[u] = 1;//正在访问该节点
        for(int v:graph[u]){
            if(visited[v]==0){
                dfs(v, graph, visited);
                if(circle)
                    return;
            }else if(visited[v]==1){
                circle = true;
                return;
            }
        }
        visited[u] = 2;
        res.push_back(u);
    }

    vector<int> findOrder(int numCourses, vector<vector<int> >& prerequisites) {
        vector<vector<int> > graph(numCourses);
        for (auto course : prerequisites)
        {//build graph
            graph[course[1]].push_back(course[0]);
        }

        vector<int> visited(numCourses);
        for (int i = 0; i < numCourses && !circle; i++)
        {
            if(!visited[i])
                dfs(i, graph, visited);
        }
        if(circle)
            return {};
        reverse(res.begin(), res.end());
        return res;
    }
  2. bfs。同上题，只需要在节点访问完成时放入结果向量。时空复杂度与上题相同。
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    vector<int> findOrder(int numCourses, vector<vector<int> >& prerequisites) {
        vector<vector<int> > graph(numCourses);
        vector<int> inDegree(numCourses, 0);
        for (auto course : prerequisites)
        {//build graph
            graph[course[1]].push_back(course[0]);
            inDegree[course[0]]++;
        }

        queue<int> que;
        for (int i = 0; i < numCourses;i++)
        {
            if(inDegree[i]==0)
                que.push(i);
        }

        vector<int> res;
        int visited = 0;
        while (!que.empty())
        {
            visited++;
            int u = que.front();
            que.pop();
            res.push_back(u);
            for (int v : graph[u])
            {
                inDegree[v]--;
                if(inDegree[v]==0)
                    que.push(v);
            }
        }
        if(visited!=numCourses)
            return {};
        return res;
    }

4.133. 克隆图（中等）

给你无向 连通 图中一个节点的引用，请你返回该图的 深拷贝（克隆）。

图中的每个节点都包含它的值 val（int） 和其邻居的列表（list[Node]）。

1
2
3
4
class Node {
    public int val;
    public List<Node> neighbors;
}

题解：

  1. bfs
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
Node* cloneGraph(Node* node) {
    if (node == nullptr) {
        return node;
    }

    unordered_map<Node*, Node*> visited;

    // 将题目给定的节点添加到队列
    queue<Node*> que;
    que.push(node);
    // 克隆第一个节点并存储到哈希表中
    visited[node] = new Node(node->val);

    // 广度优先搜索
    while (!que.empty()) {
        // 取出队列的头节点
        auto curNode = que.front();
        que.pop();
        // 遍历该节点的邻居
        for (auto& neighbor: curNode->neighbors) {
            if (visited.find(neighbor) == visited.end()) {
                // 如果没有被访问过，就克隆并存储在哈希表中
                visited[neighbor] = new Node(neighbor->val);
                // 将邻居节点加入队列中
                que.push(neighbor);
            }
            // 更新当前节点的邻居列表
            visited[curNode]->neighbors.emplace_back(visited[neighbor]);
        }
    }

    return visited[node];
}

时间复杂度：O(n)
空间复杂度：O(n)

  1. dfs
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    unordered_map<Node*, Node*> visited;

    Node* cloneGraph(Node* node) {
        if (node == nullptr) {
            return node;
        }

        if(visited.find(node) != visited.end())
            return visited[node];

        Node *cloneNode = new Node(node->val);
        visited[node] = cloneNode;

        for(auto &neighbor:node->neighbors){
            cloneNode->neighbors.push_back(cloneGraph(neighbor));
        }

        return visited[node];
    }
    时间复杂度：O(n)
    空间复杂度：O(n)

2.5 堆

1. 给一个数组h，h有n个元素；每次可以给数组h中最小的元素加x；总共可以加m次。求m次运算后的数组最小值。

示例：

1
2
3
输入：a = {1,2,3}, n = 3, x = 1, m =2

输出：2

题解：
维护一个小根堆。每次从堆顶取出最小值，加上x后在放入堆中。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int minimalAfterAdd(vector<int> &h, int n, int m, int x){
    priority_queue<int,vector<int>,greater<int> > pq;
    for(int i:h)
        pq.push(i);

    while(m>0){
        int tmp = pq.top();
        pq.pop();
        pq.push(tmp + x);
        m--;
    }

    return pq.top();
}

2. 重复数组变换

堆例题

题解：
用一个map<int,索引小根堆>来保存数组元素和索引。map是默认是按key升序。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
bool repeat(map<int, priority_queue<int,vector<int>,greater<int> > > &numMap, map<int, priority_queue<int,vector<int>,greater<int> > >::iterator &iter){
    /*检查有没有重复的元素，并返回了重复元素的 it*/
    for (auto it = numMap.begin(); it != numMap.end();it++)
    {
        if(it->second.size()>1){
            iter = it;
            return true;
        }
    }
    return false;
}

vector<int> delRepeat(vector<int> &a){
    int n = a.size();
    //map<元素，索引小根堆>
    map<int, priority_queue<int,vector<int>,greater<int> > > numMap;
    for (int i = 0; i < n; i++)
        numMap[a[i]].push(i);

    auto it = numMap.begin();
    while (repeat(numMap,it))
    {
        //it: {第一个重复的元素,索引堆}
        it->second.pop();
        int idx = it->second.top();
        it->second.pop();
        numMap[it->first * 2].push(idx);
        a[idx] *= 2;
    }

    set<int> sIdx;
    for (auto m : numMap)
    {
        if(!m.second.empty()){
            sIdx.insert(m.second.top());
        }
    }

    vector<int> res;
    for(int i:sIdx){
        res.push_back(a[i]);
    }

    return res;
}

三、算法类例题

主要从Leetcode的题中选出的代表性例题，也包括笔试或者其他资料上看到的比较好的题目。
ps: 题解使用的 cpp

3.1 分治算法（Divide and conquer）

Leetcode 241. 为运算表达式设计优先级（中等）

给定一个含有数字和运算符的字符串，为表达式添加括号，改变其运算优先级以求出不同的结果。你需要给出所有可能的组合的结果。有效的运算符号包含 +, - 以及 * 。

1
2
3
4
Input: "2-1-1" 
((2-1)-1) = 0
(2-(1-1)) = 2
Output : [0, 2]

题解：
符号分开成左右两边，递归求出左右两边的结果，再排列组合成新结果。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
vector<int> diffWaysToCompute(string s){
    vector<int> res;
    for (int i = 0; i < s.size();i++){
        if(s[i]=='+' || s[i]=='-' || s[i]=='*'){
            vector<int> left = diffWaysToCompute(s.substr(0, i));
            vector<int> right = diffWaysToCompute(s.substr(i + 1));
            for(int l:left){
                for(int r:right){
                    if(s[i]=='+'){
                        res.push_back(l + r);
                    }else if (s[i] == '-'){
                        res.push_back(l - r);
                    }
                    else if (s[i] == '*'){
                        res.push_back(l * r);
                    }
                }
            }
        }
    }
    if(res.empty())
        res.push_back(stoi(s));
    return res;
}

Leetcode 95. 不同的二叉搜索树 II（中等）

给定一个数字 n，要求生成所有值为 1…n 的二叉搜索树。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
Input: 3  
Output:  
[ 
  [1,null,3,2],  
  [3,2,null,1],  
  [3,1,null,null,2],  
  [2,1,3],  
  [1,null,2,null,3]
]

Explanation:  
The above output corresponds to the 5 unique BST's shown below:  

1         3     3      2      1  
 \       /     /      / \      \  
  3     2     1      1   3      2  
 /     /       \                 \  
2     1         2                 3

题解：
把每一个节点当作父节点，递归求解左右子数，在把每个左右子树组合起来。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};

vector<TreeNode *> generateTreesCore(int start, int end){
    if(start > end)
        return {nullptr};

    vector<TreeNode *> res;
    for (int i = start; i <= end;i++){
        vector<TreeNode *> left = generateTreesCore(start, i - 1);
        vector<TreeNode *> right = generateTreesCore(i + 1, end);
        for(auto l:left){
            for(auto r:right){
                TreeNode *root = new TreeNode(i);
                root->left = l;
                root->right = r;
                res.push_back(root);
            }
        }
    }
    return res;
}
vector<TreeNode *> generateTrees(int n){
    if(n==0)
        return {};
    return generateTreesCore(1, n);
    cout << "visual tree by debug." << endl;
}

3.2 动态规划（Dynamic programming）

递归和动态规划都是将原问题拆成多个子问题然后求解，他们之间最本质的区别是，动态规划保存了子问题的解，避免重复计算。
递归一般是自上而下——从愿问题开始，逐步往下求解；动态规划一般是自下而上——从最小子问题开始，逐步扩大问题规模。
（这里写一个动态规划算法伪代码模版）

3.2.1 斐波那契数列（fabonacci）

Leetcode 70. 爬楼梯（简单）

题目描述：有 N 阶楼梯，每次可以上一阶或者两阶，求有多少种上楼梯的方法。

题解：
dp。dp[i] 表示走到第 i 个楼梯的方法数目。第 i 个楼梯可以从第 i-1 和 i-2 个楼梯再走一步到达，走到第 i 个楼梯的方法数为走到第 i-1 和第 i-2 个楼梯的方法数之和。
dp[i] = dp[i - 1] + dp[i - 2]

  1. 空间复杂度O(n)的方法
1
2
3
4
5
6
7
int climbStairs(int n){
    vector<int> dp(n+1, 1);//dp[0]=1, dp[1]=1
    for (int i = 2; i <= n;i++)
        dp[i] = dp[i - 1] + dp[i - 2];

    return dp[n];
}

时间复杂度：O(n)
空间复杂度：O(n)

  1. 空间复杂度O(1)的方法
1
2
3
4
5
6
7
8
9
10
int climbStairs(int n){
    vector<int> dp(3, 1);//dp[0]=1, dp[1]=1
    for (int i = 2; i <= n;i++){
        dp[2] = dp[1] + dp[0];
        dp[0] = dp[1];
        dp[1] = dp[2];
    }

    return dp[1];
}

时间复杂度：O(n)
空间复杂度：O(1)

Leetcode 198. 打家劫舍（简单）

题目描述：抢劫一排住户，但是不能抢邻近的住户，求最大抢劫量。

示例：

1
2
3
4
输入：[1,2,3,1]
输出：4
解释：偷窃 1 号房屋 (金额 = 1) ，然后偷窃 3 号房屋 (金额 = 3)。
     偷窃到的最高金额 = 1 + 3 = 4 。

题解：
dp。dp[i] 表示抢到第 i 个住户时的最大抢劫量。由于不能抢劫邻近住户，如果抢劫了第 i -1 个住户，那么就不能再抢劫第 i 个住户，所以：
dp[i] = max(dp[i-2]+nums[i],dp[i-1])

1
2
3
4
5
6
7
8
9
10
11
12
13
int rob(vector<int>& nums) {
    int n = nums.size();
    if(n==0)
        return 0;
    vector<int> dp(3, 0);
    dp[1] = nums[0];
    for (int i = 2; i <= n; i++){
        dp[2] = max(dp[0] + nums[i - 1], dp[1]);
        dp[0] = dp[1];
        dp[1] = dp[2];
    }
    return dp[1];//防止只有一个元素的情况
}

时间复杂度：O(n)
空间复杂度：O(1)

Leetcode 213. House Robber II （中等）

强盗在环形街区抢劫

示例：

1
2
3
输入: [2,3,2]
输出: 3
解释: 你不能先偷窃 1 号房屋（金额 = 2），然后偷窃 3 号房屋（金额 = 2）, 因为他们是相邻的。

题解：
在上一题的基础上，分成两个数组，一个包含第一家不包含最后一家，另一个不包含第一家但包含最后一家。分别 dp 求 max。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
int helper(vector<int>& nums) {
    int n = nums.size();
    if(n==0)
        return 0;
    vector<int> dp(3, 0);
    dp[1] = nums[0];
    for (int i = 2; i <= n; i++){
        dp[2] = max(dp[0] + nums[i - 1], dp[1]);
        dp[0] = dp[1];
        dp[1] = dp[2];
    }
    return dp[1];
}

int rob(vector<int>& nums){
    if(nums.empty())
        return 0;
    if(nums.size()==1)
        return nums[0];
    vector<int> nums1(nums.begin(), nums.end() - 1);
    vector<int> nums2(nums.begin()+1, nums.end());
    return max(helper(nums1), helper(nums2));
}

时间复杂度：O(2n)
空间复杂度：O(1)

Leetcode 634. 寻找数组的错位排列（中等，会员题）

题目描述：有 N 个 信 和 信封，它们被打乱，求错误装信方式的数量（所有信封都没有装各自的信）。

题解：
定义一个数组 dp 存储错误方式数量，dp[i] 表示前 i 个信和信封的错误方式数量。

假设第 i 个信装到第 j 个信封里面，而第 j 个信装到第 k 个信封里面。根据 i 和 k 是否相等，有两种情况：

  • i == k，交换 i 和 j 的信后，它们的信和信封在正确的位置，但是其余 i-2 封信有 dp[i-2] 种错误装信的方式。
    由于 j 有 i-1 种取值，因此共有 (i-1)*dp[i-2] 种错误装信方式。
  • i != k，交换 i 和 j 的信后，第 i 个信和信封在正确的位置，其余 i-1 封信有 dp[i-1] 种错误装信方式。
    由于 j 有 i-1 种取值，因此共有 (i-1)*dp[i-1] 种错误装信方式。

dp[i] = (i-1)*dp[i-2] + (i-1)*dp[i-1]

1
2
3
4
5
6
7
8
9
10
11
12
13
int wrongLetterRank(int n){
    if(n<2)
        return n;

    vector<int> dp(3, 0);
    dp[1] = 1;
    for (int i = 2; i <= n;i++){
        dp[2] = (i - 1) * dp[0] + (i - 1) * dp[1];
        dp[0] = dp[1];
        dp[1] = dp[2];
    }
    return dp[1];
}

时间复杂度：O(n)
空间复杂度：O(1)

母牛生小牛问题

题目描述：假设农场中成熟的母牛每年都会生 1 头小母牛，并且永远不会死。第一年有 1 只小母牛，从第二年开始，母牛开始生小母牛。每只小母牛 3 年之后成熟又可以生小母牛。给定整数 N，求 N 年后牛的数量。

题解：
dp[i]表示第 i 年成熟的牛的数量：

  • dp[i] = dp[i-1] + dp[i-3]
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    int cowProduce(int n){
        if(n<=4)
            return n;

        vector<int> dp(4, 1); //dp[0] = 1;
        dp[1] = 2;
        dp[2] = 3;
        for (int i = 4; i <= n;i++){
            dp[3] = dp[2] + dp[0];
            dp[0] = dp[1];
            dp[1] = dp[2];
            dp[2] = dp[3];
        }
        return dp[2];
    }
    时间复杂度：O(n)
    空间复杂度：O(1)

3.2.2 二维dp：二维网格路径问题

Leetcode 64. 最小路径和（中等）

给定一个包含非负整数的 m x n 网格，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

示例：

1
2
3
4
5
6
7
8
输入：
[
    [1,3,1],  
    [1,5,1],  
    [4,2,1]
]
输出: 7
解释: 因为路径 1→3→1→1→1 的总和最小。

题解：

  1. 二维dp。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
int minPathSum(vector<vector<int> >& grid) {
    if(grid.empty())
        return 0;
    int m = grid.size(), n = grid[0].size();
    vector<vector<int> > dp(m, vector<int>(n,0));

    dp[0][0] = grid[0][0];
    for (int i = 1; i < m; i++)
        dp[i][0] = dp[i-1][0] + grid[i][0];
    for (int j = 1; j < n; j++)
        dp[0][j] = dp[0][j-1] + grid[0][j];
    
    for (int i = 1; i < m;i++){
        for (int j = 1; j < n;j++){
            dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];
        }
    }
    return dp[m - 1][n - 1];
}

时间复杂度：O(m*n)
空间复杂度：O(m*n)

  1. 一维dp。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
int minPathSum(vector<vector<int> >& grid) {
    if(grid.empty())
        return 0;
    int m = grid.size(), n = grid[0].size();
    vector<int> dp(n, 0);

    dp[0] = grid[0][0];
    for(int i = 1;i<n;i++)
        dp[i] = dp[i - 1] + grid[0][i];

    for (int i = 1; i < m; i++){
        for (int j = 0; j < n; j++){
            if(j == 0)
                dp[j] = dp[j] + grid[i][0];
            else
                dp[j] = min(dp[j - 1], dp[j]) + grid[i][j];
        }
    }
    return dp[n-1];
}

时间复杂度：O(m*n)
空间复杂度：O(n)

Leetcode 62. 不同路径（中等）

题目描述：统计从矩阵左上角到右下角的路径总数，每次只能向右或者向下移

  • dp[i][j] = dp[i-1][j] + dp[i][j-1] 只用一行存储，空间复杂度可以优化为O(col)
  • 也可以直接用数学公式求解，这是一个组合问题。
    机器人总共移动的次数 S=m+n-2，向下移动的次数 D=m-1，那么问题可以看成从 S 中取出 D 个位置的组合数量，这个问题的解为 C(S, D)。

题解：
一维dp。

1
2
3
4
5
6
7
8
int uniquePaths(int m, int n) {
    vector<int> dp(n + 1, 1); //dp[0]==1  最左边一列都是1
    for (int i = 1; i < m;i++){//从第二行开始
        for (int j = 1; j < n;j++)
            dp[j] = dp[j - 1] + dp[j];
    }
    return dp[n-1];
}

时间复杂度：O(m*n)
空间复杂度：O(n)

3.2.3 子序列/子集/子数组/子矩阵

！！！注意！！！：子序列 和 子串并不相等，子序列/子集可以不连续，字串是连续的。

Leetcode 303. 区域和检索 - 数组不可变（简单）

给定一个整数数组  nums，求出数组从索引 i 到 j  (i ≤ j) 范围内元素的总和，包含 i,  j 两点。

示例：

1
2
3
4
5
给定 nums = [-2, 0, 3, -5, 2, -1]，求和函数为 sumRange()

sumRange(0, 2) -> 1
sumRange(2, 5) -> -1
sumRange(0, 5) -> -3

题解：
前缀和。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class NumArray {
public:
    NumArray(vector<int>& nums) {
        sums = new int[nums.size() + 1];
        sums[0] = 0;
        for (int i = 0; i < nums.size();i++)
            sums[i + 1] = sums[i] + nums[i];
    }
    
    ~NumArray() { delete[] sums; }

    int sumRange(int i, int j) {
        return sums[j + 1] - sums[i];
    }
private:
    int *sums;
};

Leetcode 413. 等差数列划分（中等）

函数要返回数组 A 中所有为等差数组的子数组个数。

示例1：

1
2
3
A = [1, 2, 3, 4]

返回: 3, A 中有三个子等差数组: [1, 2, 3], [2, 3, 4] 以及自身 [1, 2, 3, 4]。

示例2：

1
2
3
4
5
6
7
8
A = [0, 1, 2, 3, 4]  
return: 6, for 3 arithmetic slices in A:  
[0, 1, 2],  
[1, 2, 3],  
[0, 1, 2, 3],  
[0, 1, 2, 3, 4],  
[ 1, 2, 3, 4],  
[2, 3, 4]

题解：
dp[i] 表示以 A[i] 为结尾的等差递增子区间的个数。

当 A[i] - A[i-1] == A[i-1] - A[i-2]，那么 [A[i-2], A[i-1], A[i]] 构成一个等差递增子区间。而且在以 A[i-1] 为结尾的递增子区间的后面再加上一个 A[i]，一样可以构成新的递增子区间。

dp[2] = 1
[0, 1, 2]

dp[3] = dp[2] + 1 = 2
[0, 1, 2, 3], // [0, 1, 2] 之后加一个 3
[1, 2, 3] // 新的递增子区间

dp[4] = dp[3] + 1 = 3
[0, 1, 2, 3, 4], // [0, 1, 2, 3] 之后加一个 4
[1, 2, 3, 4], // [1, 2, 3] 之后加一个 4
[2, 3, 4] // 新的递增子区间

综上，在 A[i] - A[i-1] == A[i-1] - A[i-2] 时，dp[i] = dp[i-1] + 1。因为递增子区间不一定以最后一个元素为结尾，可以是任意一个元素结尾，因此需要返回 dp 数组累加的结果。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int numberOfArithmeticSlices(vector<int>& A){
    if(A.size()<3)
        return 0;
    vector<int> dp(A.size(), 0);
    for (int i = 2; i < dp.size(); i++){
        if(A[i]-A[i-1] == A[i-1]-A[i-2])
            dp[i] = dp[i - 1] + 1;
    }
    int res = 0;
    for(auto dpi:dp){
        res += dpi;
    }
    return res;
}

时间复杂度：O(n)
空间复杂度：O(n)

Leetcode 343. 整数拆分（中等）

给定一个正整数 n，将其拆分为至少两个正整数的和，并使这些整数的乘积最大化。 返回你可以获得的最大乘积。

就是割绳子问题，剑指offer也有

For example, given n = 2, return 1 (2 = 1 + 1); given n = 10, return 36 (10 = 3 + 3 + 4).

题解：
dp。dp[i]表示 i 能分割出的最大积

当 i ≥ 2 时，假设对正整数 i 拆分出的其中一个正整数是 j(1 ≤ j < i)，则有两种情况：

  • 将 i 拆分成 j 和 i−j 的和，且 i−j 不再拆分成多个正整数，此时的乘积是 j×(i−j)；
  • 将 i 拆分成 j 和 i-j 的和，且 i−j 继续拆分成多个正整数，此时的乘积是 j×dp[i−j]。

当固定时：dp[i] = max(j * dp[i - j], j * (i - j))，所以遍历 j 的可能值，就可以求出 dp[i]

1
2
3
4
5
6
7
8
9
10
11
int integerBreak(int n){
    vector<int> dp(n+1,0);
    for (int i = 2; i <= n; i++)
    {
        for (int j = 1; j < i; j++)
        {
            dp[i] = max(dp[i], max(j * (i - j), j * dp[i - j]));
        }
    }
    return dp[n];
}

时间复杂度：O(n^2)
空间复杂度：O(n)

Leetcode 279. 完全平方数（中等）

给定正整数 n，找到若干个完全平方数（比如 1, 4, 9, 16, …）使得它们的和等于 n。你需要让组成和的完全平方数的个数最少。

For example, given n = 12, return 3 because 12 = 4 + 4 + 4;
given n = 13, return 2 because 13 = 4 + 9.

题解：
dp。dp[i]表示组成和的完全平方数最少的个数：

  • dp[i] = dp[i-sqr] + 1

可以用四平方定理减少运算次数：任何一个正整数都可以表示成不超过四个整数的平方之和

1
2
3
4
5
6
7
8
9
10
int numSquares(int n) {
    vector<int> dp(n + 1, 5); //四平方定理
    dp[0] = 0;
    for (int i = 1; i <= n;i++){
        for (int j = 1; j * j <= i;j++){
            dp[i] = min(dp[i], dp[i - j * j] + 1);
        }
    }
    return dp[n];
}

时间复杂度：O(n * √n)
空间复杂度：O(n)

Leetcode 91.解码方法（中等）

一条包含字母 A-Z 的消息通过以下方式进行了编码：

1
2
3
4
'A' -> 1
'B' -> 2
...
'Z' -> 26

给定一个只包含数字的非空字符串，请计算解码方法的总数。

Given encoded message “12”, return 2
It could be decoded as “AB” (1 2) or “L” (12). The number of ways decoding “12” is 2.

题解：
二维dp。dp[i]表示前i个字符有几种解码方式。分几种情况：

  • s[i-1]!=0 && s[i-2]==0 如“101”，最近两位为”01”不能解码，所以dp[i] = dp[i-1]
  • s[i-1]==0 && s[i-2]==0 即有两个连续的零，如“100” 则不可能转为字符，dp[i] = 0
  • dp[i-2]dp[i-1]组成的数字 >26：dp[i] = dp[i-1]
  • dp[i-2]dp[i-1]组成的数字 <=26：dp[i] = dp[i-1] + dp[i-2]
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    int numDecodings(string s){
        vector<int> dp(s.size()+1, 0);
        dp[0] = 1;
        dp[1] = s[0] == '0' ? 0 : 1;
        for (int i = 2; i <= s.size();i++){
            //s[i-1]!=0 && s[i-2]==0 如“101”，最近两位为"01"不能解码，所以dp[i] = dp[i-1];
            //s[i-1]==0 && s[i-2]==0 即有两个连续的零，如“100” 则不可能转为字符，dp[i] = 0。
            if(s[i-1]!='0')
                dp[i] = dp[i - 1];
            if(s[i-2]=='0')
                continue;
            //根据最近两位的大小判断能不能解码
            int two = stoi(s.substr(i - 2, 2)); //= (s[i - 1] - '0') * 10 + (s[i] - '0');
            if (two <= 26)
                dp[i] += dp[i - 2];
        }
        return dp[s.size()];
    }
    时间复杂度：O(n)
    空间复杂度：O(n)

一维dp。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
int numDecodings(string s){
    vector<int> dp(3, 0);
    dp[0] = 1;
    dp[1] = s[0] == '0' ? 0 : 1;
    for (int i = 2; i <= s.size();i++){
        //s[i-1]!=0 && s[i-2]==0 如“101”，最近两位为"01"不能解码，所以dp[i] = dp[i-1];
        //s[i-1]==0 && s[i-2]==0 即有两个连续的零，如“100” 则不可能转为字符，dp[i] = 0。
        dp[2] = 0;
        if(s[i - 1] != '0')
            dp[2] = dp[1];
        if (s[i - 2] == '0'){
            dp[0] = dp[1];
            dp[1] = dp[2];
            continue;
        }
        //根据最近两位的大小判断能不能解码
        int two = stoi(s.substr(i - 2, 2)); //= (s[i - 1] - '0') * 10 + (s[i] - '0');
        if (two <= 26)
            dp[2] += dp[0];
        dp[0] = dp[1];
        dp[1] = dp[2];
    }
    return dp[1];
}

时间复杂度：O(n)
空间复杂度：O(1)

和为 k 的 子序列/子数组

和为 k 的 子数组
  1. Leetcode 560. 和为K的子数组（中等）

给定一个整数数组和一个整数 k，你需要找到该数组中和为 k 的连续的子数组的个数。

示例 1 :

1
2
输入:nums = [1,1,1], k = 2
输出: 2 , [1,1] 与 [1,1] 为两种不同的情况。

题解：
前缀和。

1
2
3
4
5
6
7
8
9
10
11
12
int subArrySumCnt(vector<int> &A, int &d){
    unordered_map<int, int> umap; //key:前缀和  val:出现次数
    int pre = 0, cnt = 0;
    umap[0] = 1;
    for (int &a : A){
        pre += a;
        if(umap.find(pre-d) != umap.end())
            cnt += umap[pre - d];
        umap[pre]++;
    }
    return cnt;
}

时间复杂度：O(n)
空间复杂度：O(n)

  1. 在 1. 的基础上，输出每一个子数组

题解：
保留索引的前缀和。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
vector<vector<int> > subArrySum(vector<int> &A, int &d){
    unordered_map<int, vector<pair<int,int> > > umap; //key:前缀和  val:出现的开始和结束索引 序列
    int pre = 0;
    umap[0].push_back({0, -1});
    vector<pair<int, int> > idxs;
    for (int i = 0; i < A.size(); i++){
        pre += A[i];
        if(umap.find(pre-d) != umap.end()){
            for(auto &p : umap[pre-d])//记录满足的索引
                idxs.push_back({p.second + 1, i});
        }
        umap[pre].push_back({0, i});
    }

    vector<vector<int> > res;
    for(auto &idx : idxs){
        vector<int> tmp;
        for (int i = idx.first; i <= idx.second; i++)
            tmp.push_back(A[i]);
        res.push_back(tmp);
    }
    return res;
}
和为 k 的 子集合/子序列

题解：
剪枝回溯，当和>k时丢弃该分支。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
set<vector<int> > resSet;

void backtracking(vector<int> &pre, int preSum, int idx, vector<int> &nums, int &k){
    if(preSum > k)
        return;
    if(preSum == k){
        sort(pre.begin(), pre.end());
        resSet.insert(pre);
        return;
    }

    int curSum = preSum;
    for (int i = idx; i < nums.size(); i++){
        pre.push_back(nums[i]);
        curSum += nums[i];
        backtracking(pre, curSum, i + 1, nums, k);
        curSum -= nums[i];
        pre.erase(pre.end() - 1, pre.end());
    }
    return;
}

vector<vector<int> > subSetSum(vector<int> &nums, int &k){//子集
    vector<int> pre;
    backtracking(pre, 0, 0, nums, k);
    vector<vector<int> > res(resSet.begin(), resSet.end());
    return res;
}

递增子序列

&emsp;&emsp;已知一个序列 {S1, S2,…,Sn}，取出若干数组成新的序列 {Si1, Si2,…, Sim}，其中 i1、i2 … im 保持递增，即新序列中各个数仍然保持原数列中的先后顺序，称新序列为原序列的一个子序列。如果在子序列中，当下标 ix > iy 时，Six > Siy，称子序列为原序列的一个递增子序列。
&emsp;&emsp;定义一个数组 dp 存储最长递增子序列的长度，dp[n] 表示以 Sn 结尾的序列的最长递增子序列长度。对于一个递增子序列 {Si1, Si2,…,Sim}，如果 im < n 并且 Sim < Sn，此时 {Si1, Si2,…, Sim, Sn} 为一个递增子序列，递增子序列的长度增加 1。
&emsp;&emsp;满足上述条件的递增子序列中，长度最长的那个递增子序列就是要找的，在长度最长的递增子序列上加上 Sn 就构成了以 Sn 为结尾的最长递增子序列。
&emsp;&emsp;因此 dp[n] = max{ dp[i]+1 | Si < Sn && i < n}
&emsp;&emsp;因为在求 dp[n] 时可能无法找到一个满足条件的递增子序列，此时 {Sn} 就构成了递增子序列，需要对前面的求解方程做修改，令 dp[n] 最小为 1，即：

  • dp[n] = max{1, dp[i] + 1 | Si < Sn && i < n}
    &emsp;&emsp;对于一个长度为 N 的序列，最长递增子序列并不一定会以 SN 为结尾，因此 dp[N] 不是序列的最长递增子序列的长度，需要遍历 dp 数组找出最大值才是所要的结果，max{ dp[i] | 1 <= i <= N} 即为所求。

ref. 最长递增子序列的三种算法

  1. 以上解法的时间复杂度为 O(N2)
  2. 可以使用二分查找将时间复杂度降低为 O(NlogN)
  3. 也可以用最长公共子序列法：查找原序列和排序后的序列的最长公共自序列，具体参见链接
Leetcode 300. 最长上升（递增）子序列（中等）

给定一个无序的整数数组，找到其中最长上升子序列的长度。

题解：

  1. dp。
1
2
3
4
5
6
7
8
9
10
11
12
13
int lengthOfLIS(vector<int>& nums) {
    vector<int> dp(nums.size(), 1); //至少是自身，1个
    for (int i = 0; i < nums.size();i++){
        for (int j = 0; j < i;j++){
            if(nums[j]<nums[i])
                dp[i] = max(dp[i], dp[j] + 1);
        }
    }
    int res = 0;
    for(int n:dp)
        res = max(res, n);
    return res;
}

时间复杂度：O(n^2)
空间复杂度：O(n)

  1. 二分查找+贪心。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
int BinarySearch(vector<int> &tails,int len,int num){
    int left = 0;
    int right = len - 1;
    int mid;
    while(left<=right){
        mid = (left + right) / 2;
        if (tails[mid]>num)
            right = mid - 1;
        else if(tails[mid]<num)
            left = mid + 1;
        else
            return mid;
    }
    return left;//数组中不存在该元素，则返回该元素应该插入的位置
}
int lengthOfLIS(vector<int>& nums) {
    //tails[i]表示长度为 i+1 的最长上升子序列的末尾元素的最小值
    if(nums.empty())
        return 0;
    vector<int> tails(nums.size(), 0);
    int res = 1;
    tails[0] = nums[0];
    for (int i = 1; i < nums.size(); i++)
    {
        if(nums[i]>tails[res-1]){
            tails[res] = nums[i];
            res++;
        }else{
            int pos = BinarySearch(tails,res,nums[i]);
            tails[pos] = nums[i];
        }
    }
    return res;
}

时间复杂度：O(nlogn)
空间复杂度：O(n)

Leetcode 646. 最长数对链（中等）

给出 n 个数对。 在每一个数对中，第一个数字总是比第二个数字小。

现在，我们定义一种跟随关系，当且仅当 b < c 时，数对(c, d) 才可以跟在 (a, b) 后面。我们用这种形式来构造一个数对链。

给定一个对数集合，找出能够形成的最长数对链的长度。你不需要用到所有的数对，你可以以任何顺序选择其中的一些数对来构造。

说明：对于 (a, b) 和 (c, d) ，如果 b < c，则它们可以构成一条链。求一组整数对能够构成的最长链。

示例：

1
2
3
Input: [[1,2], [2,3], [3,4]]  
Output: 2  
Explanation: The longest chain is [1,2] -> [3,4]

题解：
和最长递增子序列很像。

  1. dp。dp[i]是以i结尾时的最长链长度：dp[i] = max{dp[j]+1 | j~(1,i) && pairs[i][0]>pairs[j][1]}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
bool cmp(vector<int> &a, vector<int> &b){
    if(a[0]==b[0])
        return a[1] < b[1];
    return a[0] < b[0];
}

int findLongestChain(vector<vector<int> >& pairs) {
    if(pairs.size()<2)
        return pairs.size();
    
    sort(pairs.begin(), pairs.end(), cmp);
    vector<int> dp(pairs.size(), 1);
    for (int i = 1; i < pairs.size(); i++){
        for (int j = 0; j < i;j++){
            if (pairs[i][0] > pairs[j][1])
                dp[i] = max(dp[i], dp[j] + 1);
        }
    }

    int res = 0;
    for(auto d:dp)
        res = max(res, d);

    return res;
}

时间复杂度：O(n^2)
空间复杂度：O(n)

  1. 二分+贪心。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
int BinarySearch(vector< vector<int> > &tails,int len,vector<int> inputPair){
    int left = 0;
    int right = len-1;
    int mid;
    while (left<=right)
    {
        mid = (left + right) / 2;
        if(tails[mid][1]<inputPair[0])
            left = mid + 1;
        else if(tails[mid][0]>inputPair[1])
            right = mid - 1;
        else
            return mid;
    }
    return left;
}

bool cmp(vector<int> &a, vector<int> &b){
    if(a[0]==b[0])
        return a[1] < b[1];
    return a[0] < b[0];
}

int findLongestChain(vector<vector<int> >& pairs) {
    if(pairs.size()<2)
        return pairs.size();
    
    sort(pairs.begin(), pairs.end(), cmp);
    vector< vector<int> > tails(pairs.size(),vector<int>(2,0));
    tails[0] = pairs[0];
    int res = 1;
    for (int i = 1; i < pairs.size();i++)
    {
        if(pairs[i][0]>tails[res-1][1]){
            tails[res] = pairs[i];
            res++;
        }else{
            int pos = BinarySearch(tails,res,pairs[i]);
            if(tails[pos][1]>pairs[i][1])
                tails[pos] = pairs[i];
        }
    }
    return res;
}

时间复杂度：O(nlogn)
空间复杂度：O(n)

Leetcode 376. 摆动序列（中等）

如果一个序列中连续的数之间的差值在正数和负数之间来回交替，那么这个序列被称作摆动序列。如果存在第一个差值的话，可能为正数或者负数。长度小于2的序列被认为是摆动序列。

例如：[1,7,4,9,2,5]为摆动序列。而[1,4,7,2,5] 和[1,7,4,5,5]不是摆动序列

给定一组数，返回最长的摆动子序列。注意序列是由原数组删除一些元素(也可以不删除)并且保留元素顺序得到的。

示例：

1
2
3
4
5
6
7
8
Input: [1,7,4,9,2,5]  
Output: 6  
The entire sequence is a wiggle sequence.  
Input: [1,17,5,10,13,15,10,5,16,8]  
Output: 7  
There are several subsequences that achieve this length. One is [1,17,10,13,10,16,8].  
Input: [1,2,3,4,5,6,7,8,9]  
Output: 2

题解：

  1. dp。用两个分别保存上升和下降的最长长度。
    • dpUp[i] 表示 i 之前上升序列最长的子序列长度
    • dpDown[i] 表示 i 之前下降序列最长的子序列长度
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
int wiggleMaxLength(vector<int>& nums) {
    if(nums.empty())
        return 0;
    vector<int> dpUp(nums.size());
    vector<int> dpDown(nums.size());
    dpUp[0] = 1;
    dpDown[0] = 1;
    for (int i = 1; i < nums.size(); i++)
    {
        if(nums[i]>nums[i-1]){//状态是上升,应该接下降，并改状态
            dpUp[i] = dpDown[i - 1] + 1;
            dpDown[i] = dpDown[i - 1];
        }else if(nums[i]<nums[i-1]){//状态是下降，应该接上升，并改状态
            dpDown[i] = dpUp[i - 1] + 1;
            dpUp[i] = dpUp[i - 1];
        }else{
            dpUp[i] = dpUp[i - 1];
            dpDown[i] = dpDown[i - 1];
        }
    }
    int res = 0;
    for(auto d:dpUp)
        res = max(res, d);
    for(auto d:dpDown)
        res = max(res, d);
    return res;
}

时间复杂度：O(2n)
空间复杂度：O(2n)

  1. 因为只用到了前一个值，所以可以优化空间复杂度。
1
2
3
4
5
6
7
8
9
10
11
12
int wiggleMaxLength(vector<int>& nums) {
    if(nums.empty())
        return 0;
    int up = 1, down = 1;
    for (int i = 1; i < nums.size();i++){
        if(nums[i]>nums[i-1])
            up = down + 1;
        else if(nums[i]<nums[i-1])
            down = up + 1;
    }
    return max(up, down);
}

时间复杂度：O(n)
空间复杂度：O(1)

公共子序列

dp[i][j] 表示 S1 的前 i 个字符与 S2 的前 j 个字符最长公共子序列的长度。

考虑 S1[i] 与 S2j 值是否相等，分为两种情况：

  • 当 S1[i] == S2[j] 时，那么就能在 S1 的前 i-1 个字符与 S2 的前 j-1 个字符最长公共子序列的基础上再加上 S1i 这个值，
    最长公共子序列长度加 1，即 dp[i][j] = dp[i-1][j-1] + 1。
  • 当 S1[i] != S2[j] 时，此时最长公共子序列为 S1 的前 i-1 个字符和 S2 的前 j 个字符最长公共子序列，
    或者 S1 的前 i 个字符和 S2 的前 j-1 个字符最长公共子序列，取它们的最大者，
    即 dp[i][j] = max{dp[i-1][j], dp[i][j-1]}。

对于长度为 N 的序列 S1 和长度为 M 的序列 S2，dp[N][M] 就是序列 S1 和序列 S2 的最长公共子序列长度。

Leetcode 1143. 最长公共子序列Longest Common Subsequence（中等）

求最长公共子序列

示例：

1
2
3
输入：text1 = "abcde", text2 = "ace" 
输出：3  
解释：最长公共子序列是 "ace"，它的长度为 3。

题解：

  1. 二维dp。dp[i][j]表示第一个字符串的前 i 个和第二个字符串的前 j 个字符的LCS。
    • 当s1[i-1] == s2[j-1]时，dp[i][j] = dp[i - 1][j - 1] + 1
    • 当s1[i-1] != s2[j-1]时，dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int longestCommonSubsequence(string text1, string text2) {
    if(text1.size()==0||text2.size()==0)
        return 0;
    
    vector< vector<int> > dp(text1.size()+1,vector<int>(text2.size()+1));
    for (int i = 1; i <= text1.size();i++){
        for (int j = 1; j <= text2.size();j++){
            if(text2[j-1]==text1[i-1])
                dp[i][j] = dp[i - 1][j - 1] + 1;
            else
                dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
        }
    }
    return dp[text1.size()][text2.size()];
}

时间复杂度：O(mn)
空间复杂度：O(mn)

  1. 一维dp。注意：使用一维dp的时候，需要上一行的前一个数，所以不能使用上一个数和前一个数更新，还要保留上一行。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int longestCommonSubsequence(string text1, string text2) {
    if(text1.size()==0||text2.size()==0)
        return 0;
    
    vector<int> dp(text2.size()+1, 0);
    vector<int> last(text2.size()+1, 0);
    for (int i = 1; i <= text1.size();i++){
        for (int j = 1; j <= text2.size();j++){
            if(text2[j-1]==text1[i-1])
                dp[j] = last[j - 1] + 1;
            else
                dp[j] = max(last[j], dp[j - 1]);
        }
        last = dp;
    }
    return dp[text2.size()];
}

时间复杂度：O(mn)
空间复杂度：O(2n)

Leetcode 583. 两个字符串的删除操作（中等）

给定两个单词 word1 和 word2，找到使得 word1 和 word2 相同所需的最小步数，每步可以删除任意一个字符串中的一个字符。

示例：

1
2
3
输入: "sea", "eat"
输出: 2
解释: 第一步将"sea"变为"ea"，第二步将"eat"变为"ea"

题解：
其实就是算最长公共子序列。

  1. 二维dp
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
int minDistance(string word1, string word2) {
    if(word1.empty())
        return word2.size();
    if(word2.empty())
        return word1.size();

    int m = word1.size(), n = word2.size();
    vector<vector<int> > dp(m+1,vector<int>(n+1, 0));
    for(int i=1;i<=m;i++){
        for(int j=1;j<=n;j++){
            if(word1[i-1]==word2[j-1])
                dp[i][j] = dp[i-1][j-1]+1;
            else
                dp[i][j] = max(dp[i-1][j],dp[i][j-1]);
        }
    }
    return m+n-2*dp[m][n];
}

时间复杂度：O(mn)
空间复杂度：O(mn)

  1. 一维dp。注意：使用一维dp的时候，需要上一行的前一个数，所以不能使用上一个数和前一个数更新，还要保留上一行。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
int minDistance(string word1, string word2) {
    if(word1.empty())
        return word2.size();
    if(word2.empty())
        return word1.size();

    int m = word1.size(), n = word2.size();
    vector<int> dp(n+1);
    vector<int> last(n+1);
    for(int i=1;i<=m;i++){
        for (int j = 1; j <= n; j++)
        {
            if (word1[i - 1] == word2[j - 1])
                dp[j] = last[j-1] + 1;
            else
                dp[j] = max(last[j],dp[j-1]);
        }
        last = dp;
    }
    return m+n-2*dp[n];
}

时间复杂度：O(mn)
空间复杂度：O(2n)

最大连续子数组

Leetcode 53. 最大子序和（简单）

给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

示例:

1
2
3
输入: [-2,1,-3,4,-1,2,1,-5,4]
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大，为 6。

题解：
dp。优化空间复杂度为O(1)。

1
2
3
4
5
6
7
8
int maxSubArray(vector<int>& nums) {
    int pre = 0, res = nums[0];
    for (const auto &x: nums) {
        pre = max(pre + x, x);
        res = max(res, pre);
    }
    return res;
}

时间复杂度：O(n)
空间复杂度：O(1)

返回最大子数组

在上题的基础上，要返回这个最大子数组，不只是和。

题解：
对于dp[i]=max(dp[i-1]+nums[i], nums[i])

  • 当dp[i-1]<0时，nums[i]大
  • 当dp[i-1]>0时，dp[i-1]+nums[i]大
    因为要返回数组，所以在状态转移时需要更新一下开始索引。
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    vector<int> maxSubArray(vector<int>& nums) {
        int pre = nums[0], start = 0;
        int maxSum = INT_MIN;
        vector<int> resIdx(2);
        for (int i = 1; i < nums.size(); i++)
        {
            if(pre > 0){ //如果返回最长的子数组，这个就应该是 if(pre >= 0)
                pre = pre + nums[i];
            }else{//子数组的开始索引要更新了
                pre = nums[i];
                start = i;
            }
            if(pre > maxSum){//更新答案
                maxSum = pre;
                resIdx[0] = start;
                resIdx[1] = i;
            }
        }

        vector<int> res;
        for (int i = resIdx[0]; i <= resIdx[1]; i++){
            res.push_back(nums[i]);
        }
        return res;
    }
    时间复杂度：O(n)
    空间复杂度：O(1)

旋转数组的最大连续子数组

旋转连续子数组和

给定一个旋转数组nums，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

注意：

1
2
旋转数组为首位相连的数组，如：
[1,2,3] 的子数组有 [1,2],[2,3],[3,1]

题解：
以[2,1,3]为例，最大子数组可能位于 中间(如[1,3]) 或者 两边([3,2])。

  • 若最大子数组在中间，则用上题方法可得；
  • 若最大子数组在两边，使用dp求出位于中间的最小子数组的和，就得到了位于两边的最大子数组和。因为数组和是一定的，中间的子数组和越小，位于两边的子数组和越大。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
int maxSubArray(vector<int>& nums){
    //位于中间 最大和 的 子数组
    int pre = 0, maxMid = nums[0];
    for (const int n : nums)
    {
        pre = max(n, pre + n);
        maxMid = max(maxMid, pre);
    }

    //位于两边 最大和 的 子数组
    //中间最小和
    pre = nums[0];
    int minMid = nums[0], sumn = nums[0];
    for (int i = 1; i < nums.size(); i++)
    {
        pre = min(nums[i], pre + nums[i]);
        minMid = min(minMid, pre);
        sumn += nums[i];
    }
    int maxSide = sumn - minMid; //两边 最大和

    return maxMid > maxSide ? maxMid : maxSide;
}

时间复杂度：O(n)
空间复杂度：O(1)

返回最大和的旋转连续子数组

给定一个旋转数组nums，返回一个具有最大和的连续子数组，不只是和。
题解：
在上题状态转移的基础上，增加了索引的记录。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
vector<int> maxSubArray(vector<int>& nums) {
    //位于中间 最大和 的 子数组
    int pre = nums[0], start = 0;
    int maxMid = INT_MIN;    
    vector<int> maxIdx(2);
    for (int i = 1; i < nums.size(); i++)
    {
        if(pre > 0){ //如果返回最长的子数组，这个就应该是 if(pre >= 0)
            pre = pre + nums[i];
        }else{//子数组的开始索引要更新了
            pre = nums[i];
            start = i;
        }
        if(pre > maxMid){//更新答案
            maxMid = pre;
            maxIdx[0] = start;
            maxIdx[1] = i;
        }
    }

    //位于两边 最大和 的 子数组
    //中间最小和
    pre = nums[0]; start = 0;
    int minMid = nums[0], sumn = nums[0];
    vector<int> minIdx(2);
    for (int i = 1; i < nums.size(); i++)
    {
        sumn += nums[i];
        if(pre < 0){
            pre = pre + nums[i];
        }else{
            pre = nums[i];
            start = i;
        }
        if(pre < minMid){
            minMid = pre;
            minIdx[0] = start;
            minIdx[1] = i;
        }
    }

    vector<int> resIdx(2);
    vector<int> res;
    if(maxMid > (sumn - minMid)){//子数组在中间
        resIdx = maxIdx;

        for (int i = resIdx[0]; i <= resIdx[1]; i++){
            res.push_back(nums[i]);
        }
    }
    else{//子数组在两边
        resIdx[0] = (minIdx[1] + 1) % nums.size();
        resIdx[1] = (minIdx[0] - 1 + nums.size()) % nums.size();

        for (int i = resIdx[0]; i < nums.size(); i++){
            res.push_back(nums[i]);
        }
        for (int i = 0; i <= resIdx[1]; i++){
            res.push_back(nums[i]);
        }
    }

    return res;
}

时间复杂度：O(n)
空间复杂度：O(1)

二维矩阵最大子矩阵和

最大子矩阵和

给定一个正整数和负整数组成的矩阵matrix，返回元素总和最大的子矩阵。

题解：
我们在前面已经会求最大子数组和，最大矩阵和只需要把二维矩阵压缩为一维数组，再用之前求最大子数组和的方法，就可以得到最大矩阵和。

我们把矩阵垂直压缩成一维数组，如：

1
2
3
4
5
6
7
8
9
matrix = [[1,2,3],
          [1,2,3]]

可以压缩成：nums = [2,4,6]

其中: 
nums[0] = matrix[0][0] + matrix[1][0]
nums[1] = matrix[0][1] + matrix[1][1]
nums[2] = matrix[0][2] + matrix[1][2]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
int maxSubArray(vector<int>& nums) {
    int pre = 0, res = nums[0];
    for (const auto &x: nums) {
        pre = max(pre + x, x);
        res = max(res, pre);
    }
    return res;
}

int maxSubMatrix(vector<vector<int> > &matrix){
    if(matrix.empty())
        return 0;
    int rows = matrix.size();
    int cols = matrix[0].size();

    int res = INT_MIN;
    for (int up = 0; up < rows; up++)//上界
    {
        vector<int> nums(cols, 0);//压缩为一维数组
        for (int buttom = up; buttom < rows; buttom++)//下界
        {
            for (int i = 0; i < cols;i++)//每次往下一行，就只需在之前的nums上加上这一行
                nums[i] += matrix[buttom][i];

            int maxArr = maxSubArray(nums);
            res = max(maxArr, res);
        }
    }
    return res;
}
返回最大子矩阵

在更新最大和的时候记录左上角和右下角的索引。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
int maxSubArray(vector<int>& nums, vector<int> &maxIdx) {
    int pre = nums[0], start = 0;
    int maxSum = INT_MIN;
    for (int i = 1; i < nums.size(); i++)
    {
        if(pre > 0){ //如果返回最长的子数组，这个就应该是 if(pre >= 0)
            pre = pre + nums[i];
        }else{//子数组的开始索引要更新了
            pre = nums[i];
            start = i;
        }
        if(pre > maxSum){//更新答案
            maxSum = pre;
            maxIdx[0] = start;
            maxIdx[1] = i;
        }
    }

    return maxSum;
}

vector<vector<int> > maxSubMatrix(vector<vector<int> > &matrix){
    if(matrix.empty())
        return matrix;
    int rows = matrix.size();
    int cols = matrix[0].size();

    int maxArr = INT_MIN;
    vector<int> maxIdx(4);//0上、1左、2下、3右
    for (int up = 0; up < rows; up++)//上界
    {
        vector<int> nums(cols, 0);//压缩为一维数组
        for (int down = up; down < rows; down++)//下界
        {
            for (int i = 0; i < cols;i++)//每次往下一行，就只需在之前的nums上加上这一行
                nums[i] += matrix[down][i];

            vector<int> tmpIdx(2);
            int tmp = maxSubArray(nums, tmpIdx);
            if(tmp > maxArr){
                maxArr = tmp;
                maxIdx[0] = up;
                maxIdx[1] = tmpIdx[0];
                maxIdx[2] = down;
                maxIdx[3] = tmpIdx[1];
            }
        }
    }

    int subRows = maxIdx[2] - maxIdx[0] + 1;
    int subCols = maxIdx[3] - maxIdx[1] + 1;
    vector<vector<int> > res(subRows,vector<int>(subCols));
    for (int row = maxIdx[0], i = 0; row <= maxIdx[2]; row++, i++)
    {
        for (int col = maxIdx[1], j = 0; col <= maxIdx[3]; col++, j++)
        {
            res[i][j] = matrix[row][col];
        }
    }
    return res;
}

二维矩阵最大旋转子矩阵

最旋转大子矩阵和

给定一个正整数和负整数组成的旋转矩阵matrix，返回元素总和最大的子矩阵。

题解：
只需要把上题求最大子数组和的函数换为上面提到的最大旋转子数组的函数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
int maxSubArray(vector<int>& nums){
    //位于中间 最大和 的 子数组
    int pre = 0, maxMid = nums[0];
    for (const int n : nums)
    {
        pre = max(n, pre + n);
        maxMid = max(maxMid, pre);
    }

    //位于两边 最大和 的 子数组
    //中间最小和
    pre = nums[0];
    int minMid = nums[0], sumn = nums[0];
    for (int i = 1; i < nums.size(); i++)
    {
        pre = min(nums[i], pre + nums[i]);
        minMid = min(minMid, pre);
        sumn += nums[i];
    }
    int maxSide = sumn - minMid;

    return maxMid > maxSide ? maxMid : maxSide;
}

int maxSubMatrix(vector<vector<int> > &matrix){
    if(matrix.empty())
        return 0;
    int rows = matrix.size();
    int cols = matrix[0].size();

    int res = INT_MIN;
    for (int up = 0; up < rows; up++)//上界
    {
        vector<int> nums(cols, 0);//压缩为一维数组
        for (int buttom = up; buttom < rows; buttom++)//下界
        {
            for (int i = 0; i < cols;i++)//每次往下一行，就只需在之前的nums上加上这一行
                nums[i] += matrix[buttom][i];

            int maxArr = maxSubArray(nums);
            res = max(maxArr, res);
        }
    }
    return res;
}
返回最大旋转子矩阵

在上题的基础上记录坐标。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
int maxSubArray(vector<int>& nums, vector<int> &resIdx) {
    //位于中间 最大和 的 子数组
    int pre = nums[0], start = 0;
    int maxMid = INT_MIN;    
    vector<int> maxIdx(2);
    for (int i = 1; i < nums.size(); i++)
    {
        if(pre > 0){ //如果返回最长的子数组，这个就应该是 if(pre >= 0)
            pre = pre + nums[i];
        }else{//子数组的开始索引要更新了
            pre = nums[i];
            start = i;
        }
        if(pre > maxMid){//更新答案
            maxMid = pre;
            maxIdx[0] = start;
            maxIdx[1] = i;
        }
    }

    //位于两边 最大和 的 子数组
    //中间最小和
    pre = nums[0]; start = 0;
    int minMid = nums[0], sumn = nums[0];
    vector<int> minIdx(2);
    for (int i = 1; i < nums.size(); i++)
    {
        sumn += nums[i];
        if(pre < 0){
            pre = pre + nums[i];
        }else{
            pre = nums[i];
            start = i;
        }
        if(pre < minMid){
            minMid = pre;
            minIdx[0] = start;
            minIdx[1] = i;
        }
    }

    int maxArr = sumn - minMid;
    if (maxMid > maxArr){ //子数组在中间
        resIdx = maxIdx;
        maxArr = maxMid;
    }else{//子数组在两边
        resIdx[0] = (minIdx[1] + 1) % nums.size();
        resIdx[1] = (minIdx[0] - 1 + nums.size()) % nums.size();
    }

    return maxArr;
}

vector<vector<int> > maxSubMatrix(vector<vector<int> > &matrix){
    if(matrix.empty())
        return matrix;
    int rows = matrix.size();
    int cols = matrix[0].size();

    int maxArr = INT_MIN;
    vector<int> maxIdx(4);//0上、1左、2下、3右
    for (int up = 0; up < rows; up++)//上界
    {
        vector<int> nums(cols, 0);//压缩为一维数组
        for (int down = up; down < rows; down++)//下界
        {
            for (int i = 0; i < cols;i++)//每次往下一行，就只需在之前的nums上加上这一行
                nums[i] += matrix[down][i];

            vector<int> tmpIdx(2);
            int tmp = maxSubArray(nums, tmpIdx);
            if(tmp > maxArr){
                maxArr = tmp;
                maxIdx[0] = up;
                maxIdx[1] = tmpIdx[0];
                maxIdx[2] = down;
                maxIdx[3] = tmpIdx[1];
            }
        }
    }

    int subRows = maxIdx[2] - maxIdx[0] + 1;
    vector<vector<int> > res;
    if (maxIdx[3] >= maxIdx[1])
    { //子矩阵在中间
        int subCols = maxIdx[3] - maxIdx[1] + 1;
        // vector<int> tmpVec(subCols);
        res.resize(subRows, vector<int>(subCols));
        for (int row = maxIdx[0], i = 0; row <= maxIdx[2]; row++, i++){
            for (int col = maxIdx[1], j = 0; col <= maxIdx[3]; col++, j++)
                res[i][j] = matrix[row][col];
        }
    }
    else
    { //子矩阵在两边
        int subCols = cols - (maxIdx[1] - maxIdx[3] - 1);
        res.resize(subRows,vector<int>(subCols));
        for (int row = maxIdx[0], i = 0; row <= maxIdx[2]; row++, i++){
            int j = 0;
            for (int col = maxIdx[1]; col < cols; col++, j++)
                res[i][j] = matrix[row][col];
            for (int col = 0; col <= maxIdx[3]; col++,j++)
                res[i][j] = matrix[row][col];
        }
    }
    return res;
}

3.2.4 0-1背包问题

&emsp;&emsp;有一个容量为 N 的背包，要用这个背包装下物品的价值最大，这些物品有两个属性：体积 w 和价值 v。定义一个二维数组 dp 存储最大价值，其中 dp[i][j] 表示前 i 件物品体积不超过 j 的情况下能达到的最大价值。
&emsp;设第 i 件物品体积为 w，价值为 v，根据第 i 件物品是否添加到背包中，可以分两种情况讨论：

  • 第 i 件物品没添加到背包，总体积不超过 j 的前 i 件物品的最大价值
    就是总体积不超过 j 的前 i-1 件物品的最大价值，dp[i][j] = dp[i-1][j]。
  • 第 i 件物品添加到背包中，dp[i][j] = dp[i-1][j-w] + v。

&emsp;&emsp;第 i 件物品可添加也可以不添加，取决于哪种情况下最大价值更大。因此，0-1 背包的状态转移方程为：

  • dp[i][j]=max(dp[i-1][j],dp[i-1][j-w]+v)

二维dp 0-1 背包

dp[i][j]表示前 i 件物品体积不超过 j 的情况下能达到的最大价值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int knapsack(vector<vector<int> > &nums, int N){
    //nums = { {5,12},{4,3},{7,10},{2,3},{6,6} };//{wight,val}
    //N = 15;
    vector<vector<int> > dp(nums.size()+1,vector<int>(N+1));
    for (int i = 1; i <= nums.size(); i++)
    {
        for (int j = 1; j <= N;j++){
            int weight = nums[i - 1][0];
            int val = nums[i - 1][1];
            if (j >= weight)
                dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight] + val);
            else
                dp[i][j] = dp[i - 1][j];
        }
    }
    return dp[nums.size()][N];
}

时间复杂度：O(mn)
空间复杂度：O(mn)

空间优化：一维dp 0-1 背包

观察状态转移方程可以知道，前 i 件物品的状态仅与前 i-1 件物品的状态有关，因此可以将 dp 定义为一维数组，其中 dp[j] 既可以表示 dp[i-1][j] 也可以表示 dp[i][j]。

  • d[j] = max(d[j],d[j-w]+v)

因为 dp[j-w] 表示 dp[i-1][j-w]，因此不能先求 dp[i][j-w]，防止将 dp[i-1][j-w] 覆盖。也就是说要先计算 dp[i][j] 再计算 dp[i][j-w]，在程序实现时需要按倒序来循环求解。

1
2
3
4
5
6
7
8
9
10
11
12
int knapsack(vector<vector<int> > &nums, int N){
    vector<int> dp(N+1);
    for (int i = 1; i <=nums.size();i++){
        int weight = nums[i - 1][0];
        int val = nums[i - 1][1];
        for (int j = N; j >= 1;j--){
            if(j>=weight)
                dp[j] = max(dp[j], dp[j - weight] + val);
        }
    }
    return dp[N];
}

时间复杂度：O(mn)
空间复杂度：O(n)

Leetcode 416. 分割等和子集（中等）

给定一个只包含正整数的非空数组。是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。

示例： 

1
2
3
Input: [1, 5, 11, 5]  
Output: true  
Explanation: The array can be partitioned as [1, 5, 5] and [11].

题解：
可以看成一个背包大小为 sum/2 的 0-1 背包问题。

  1. 二维dp。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
bool canPartition(vector<int>& nums) {
    int sum = 0;
    for (int i = 0; i < nums.size();i++)
        sum += nums[i];
    if(sum & 1)//奇数
        return false;
    int W = sum / 2;

    vector<vector<bool> > dp(nums.size()+1,vector<bool>(W+1,false));
    for (int m = 0; m < nums.size();m++)
        dp[m][0] = true;
    for (int i = 1; i <= nums.size(); i++)
    {
        for (int j = 1; j <= W; j++)
        {
            dp[i][j] = dp[i - 1][j];
            if((!dp[i][j]) && j>=nums[i-1])
                dp[i][j] = dp[i - 1][j - nums[i - 1]];
        }
    }
    return dp[nums.size()][W];
}
  1. 一维dp。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
bool canPartition(vector<int>& nums) {
    int sum = 0;
    for (int i = 0; i < nums.size();i++)
        sum += nums[i];
    if(sum & 1)//奇数
        return false;
    int W = sum / 2;

    vector<bool> dp1(W + 1,false);
    dp1[0] = true;
    for(auto num:nums){
        for (int j = W; j >= num;j--)
            dp1[j] = dp1[j] || dp1[j - num];
    }
    return dp1[W];
}

leetcode 494. 目标和（中等）

给定一个非负整数数组，a1, a2, …, an, 和一个目标数，S。现在你有两个符号 + 和 -。对于数组中的任意一个整数，你都可以从 + 或 -中选择一个符号添加在前面。

返回可以使最终数组和为目标数 S 的所有添加符号的方法数。

示例： 

1
2
3
4
5
6
7
8
9
Input: nums is [1, 1, 1, 1, 1], S is 3.  
Output: 5   
Explanation:  
-1+1+1+1+1 = 3  
+1-1+1+1+1 = 3  
+1+1-1+1+1 = 3  
+1+1+1-1+1 = 3  
+1+1+1+1-1 = 3  
There are 5 ways to assign symbols to make the sum of nums be target 3.

题解：
该问题可以转换为 Subset Sum 问题，从而使用 0-1 背包的方法来求解。

可以将这组数看成两部分，P 和 N，其中 P 使用正号，N 使用负号，有以下推导：

  • sum(P) - sum(N) = target
  • sum(P) + sum(N) + sum(P) - sum(N) = target + sum(P) + sum(N)
  • 2 * sum(P) = target + sum(nums)

因此只要找到一个子集，令它们都取正号，并且和等于 (target + sum(nums))/2，就证明存在解。

1
2
3
4
5
6
7
8
9
10
11
12
13
int findTargetSumWays(vector<int>& nums, int S) {
    long sum = 0;
    for (const int &num : nums) sum += num;
    if ((S + sum) % 2 == 1 || S > sum) return 0;
    S = (S + sum) / 2;
    vector<int> dp(S+1);
    dp[0] = 1;
    for (const int &num : nums) {
        for (int j = S; j >= num; j--)
            dp[j] += dp[j - num];
    }
    return dp[S];
}

时间复杂度：O(nW)
空间复杂度：O(W)

0-1 背包问题无法使用贪心算法的解释

0-1 背包问题无法使用贪心算法来求解，也就是说不能按照先添加性价比最高的物品来达到最优，这是因为这种方式可能造成背包空间的浪费，从而无法达到最优。考虑下面的物品和一个容量为 5 的背包，如果先添加物品 0 再添加物品 1，那么只能存放的价值为 16，浪费了大小为 2 的空间。最优的方式是存放物品 1 和物品 2，价值为 22.

id w v v/w
0 1 6 6
1 2 10 5
2 3 12 4

变种

  • 完全背包：物品数量为无限个
  • 多重背包：物品数量有限制
  • 多维费用背包：物品不仅有重量，还有体积，同时考虑这两种限制
  • 其它：物品之间相互约束或者依赖

3.2.5 股票问题

Leetcode 121. 买卖股票的最佳时机（简单）

给定一个数组，它的第 i 个元素是一支给定股票第 i 天的价格。

如果你最多只允许完成一笔交易（即买入和卖出一支股票一次），设计一个算法来计算你所能获取的最大利润。

示例：

1
2
3
4
输入: [7,1,5,3,6,4]
输出: 5
解释: 在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
     注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格；同时，你不能在买入前卖出股票。

题解：
用minPrices来记录历史最低价，res目前的最大收益。

1
2
3
4
5
6
7
8
9
10
int maxProfit(vector<int>& prices) {
    if(prices.empty())
        return 0;
    int minPrices = prices[0], res = 0;
    for(int &p:prices){
        res = max(res, p - minPrices);
        minPrices = min(p,minPrices);
    }
    return res;
}

时间复杂度：O(n)
空间复杂度：O(1)

Leetcode 122. 买卖股票的最佳时机 II（简单）

给定一个数组，它的第 i 个元素是一支给定股票第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易（多次买卖一支股票）。

示例： 

1
2
3
4
输入: [7,1,5,3,6,4]
输出: 7
解释: 在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
     随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候卖出, 这笔交易所能获得利润 = 6-3 = 3

题解：

  1. 贪心。只要第二天价格有上升，就可以获利。
1
2
3
4
5
6
7
8
int maxProfit(vector<int>& prices) {
    int res = 0;
    for (int i = 1; i < prices.size(); i++) {
        if (prices[i] > prices[i - 1])
            res += prices[i] - prices[i - 1];
    }
    return res;
}

时间复杂度：O(n)
空间复杂度：O(1)

  1. 空间优化dp。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
int maxProfit(vector<int>& prices) {
    if (prices.empty())
        return 0;

    int dp0 = 0, dp1 = -prices[0];
    int n = prices.size();
    for (int i = 1; i < n; i++) {
        int dp0_new = max(dp0, dp1 + prices[i]);
        int dp1_new = max(dp1, dp0 - prices[i]);
        dp0 = dp0_new;
        dp1 = dp1_new;
    }
    return dp0;
}

时间复杂度：O(n)
空间复杂度：O(1)

Leetcode 123. 买卖股票的最佳时机 III（困难）

给定一个数组，它的第 i 个元素是一支给定的股票在第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。

示例：

1
2
3
4
5
6
7
8
9
10
11
输入: [3,3,5,0,0,3,1,4]  
输出: 6  
解释: 在第 4 天（股票价格 = 0）的时候买入，在第 6 天（股票价格 = 3）的时候卖出，这笔交易所能获得利润 = 3-0 = 3。随后，在第 7 天（股票价格 = 1）的时候买入，在第 8 天 （股票价格 = 4）的时候卖出，这笔交易所能获得利润 = 4-1 = 3 。  

输入: [1,2,3,4,5]  
输出: 4  
解释: 在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出,这笔交易所能获得利润 = 5-1 = 4。`注意`你不能在第 1 天和第 2 天接连购买股票，之后再将它们卖出。因为这样属于同时参与了多笔交易，你必须在再次购买前出售掉之前的股票。  

输入: [7,6,4,3,1]   
输出: 0   
解释: 在这个情况下, 没有交易完成, 所以最大利润为 0。

题解：

  1. dp。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
int maxProfit(vector<int>& prices) {
    if (prices.empty())
        return 0;
    
    int n = prices.size();
    vector<vector<vector<int> > > dp(n,vector<vector<int> >(3, vector<int>(2)));
    dp[0][1][0] = 0;
    dp[0][1][1] = -prices[0];
    dp[0][2][0] = 0;
    dp[0][2][1] = -prices[0];
    for (int i = 1; i < n; i++) {
        dp[i][2][0] = max(dp[i - 1][2][0], dp[i - 1][2][1] + prices[i]);
        dp[i][2][1] = max(dp[i - 1][2][1], dp[i - 1][1][0] - prices[i]);
        dp[i][1][0] = max(dp[i - 1][1][0], dp[i - 1][1][1] + prices[i]);
        dp[i][1][1] = max(dp[i - 1][1][1], dp[i - 1][0][0] - prices[i]);
    }
    return dp[n - 1][2][0];
}

时间复杂度：O(n)
空间复杂度：O(n)

  1. 空间优化dp
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int maxProfit(vector<int>& prices) {
    if (prices.empty())
        return 0;
    
    int n = prices.size();
    int dp10 = 0;
    int dp11 = -prices[0];
    int dp20 = 0;
    int dp21 = -prices[0];
    for (int i = 1; i < n; i++) {
        dp20 = max(dp20, dp21 + prices[i]);
        dp21 = max(dp21, dp10 - prices[i]);
        dp10 = max(dp10, dp11 + prices[i]);
        dp11 = max(dp11, -prices[i]);
    }
    return dp20;
}

时间复杂度：O(n)
空间复杂度：O(1)

Leetcode 188. 买卖股票的最佳时机 IV（困难）

给定一个数组，它的第 i 个元素是一支给定的股票在第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。

示例：

1
2
3
输入: [2,4,1], k = 2
输出: 2
解释: 在第 1 天 (股票价格 = 2) 的时候买入，在第 2 天 (股票价格 = 4) 的时候卖出，这笔交易所能获得利润 = 4-2 = 2 。

题解：
一个有收益的交易至少需要两天（在前一天买入，在后一天卖出，前提是买入价格低于卖出价格）。如果股票价格数组的长度为 n，则有收益的交易的数量最多为 n / 2（整数除法）。因此 k 的临界值是 n / 2。如果给定的 k 不小于临界值，即 k >= n / 2，则可以将 k 扩展为正无穷，此时问题等价于Leetcode 122。

其中用到了函数重载。

  1. dp。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
int maxProfit(vector<int>& prices) {
    int res = 0;
    for (int i = 1; i < prices.size(); i++) {
        if (prices[i] > prices[i - 1])
            res += prices[i] - prices[i - 1];
    }
    return res;
}
int maxProfit(int k, vector<int>& prices) {
    if (prices.empty())
        return 0;

    int n = prices.size();
    if (k >= n / 2)
        return maxProfit(prices);

    vector<vector<vector<int> > > dp(n,vector<vector<int> >(k+1, vector<int>(2)));
    for (int i = 1; i <= k; i++) {
        dp[0][i][0] = 0;
        dp[0][i][1] = -prices[0];
    }
    for (int i = 1; i < n; i++) {
        for (int j = k; j > 0; j--) {
            dp[i][j][0] = max(dp[i - 1][j][0], dp[i - 1][j][1] + prices[i]);
            dp[i][j][1] = max(dp[i - 1][j][1], dp[i - 1][j - 1][0] - prices[i]);
        }
    }
    return dp[n - 1][k][0];
}

时间复杂度：O(nk)
空间复杂度：O(nk)

  1. 空间优化。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
int maxProfit(vector<int>& prices) {
    int res = 0;
    for (int i = 1; i < prices.size(); i++) {
        if (prices[i] > prices[i - 1])
            res += prices[i] - prices[i - 1];
    }
    return res;
}
int maxProfit(int k, vector<int>& prices) {
    if (prices.empty())
        return 0;

    int n = prices.size();
    if (k >= n / 2)
        return maxProfit(prices);


    vector<vector<int> > dp(k+1, vector<int>(2));
    for (int i = 1; i <= k; i++) {
        dp[i][0] = 0;
        dp[i][1] = -prices[0];
    }
    for (int i = 1; i < n; i++) {
        for (int j = k; j > 0; j--) {
            dp[j][0] = max(dp[j][0], dp[j][1] + prices[i]);
            dp[j][1] = max(dp[j][1], dp[j - 1][0] - prices[i]);
        }
    }
    return dp[k][0];
}

时间复杂度：O(nk)
空间复杂度：O(n)

Leetcode 309. 最佳买卖股票时机含冷冻期（中等）

给定一个整数数组，其中第 i 个元素代表了第 i 天的股票价格 。​

设计一个算法计算出最大利润。在满足以下约束条件下，你可以尽可能地完成更多的交易（多次买卖一支股票）:

  • 你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。
  • 卖出股票后，你无法在第二天买入股票 (即冷冻期为 1 天)。

示例：

1
2
3
输入: [1,2,3,0,2]  
输出: 3   
解释: 对应的交易状态为: [买入, 卖出, 冷冻期, 买入, 卖出]

题解：

  1. dp。dp[i]表示第 i 天结束之后的累计最大收益。
    • dp[i][0]表示目前持有一支股票，对应的累计最大收益
    • dp[i][1]表示目前不持有任何股票，并且处于冷冻期中，对应的累计最大收益
    • dp[i][2]表示目前不持有任何股票，并且不处于冷冻期中，对应的累计最大收益
1
2
3
4
5
6
7
8
9
10
11
12
int maxProfit(vector<int>& prices) {
    if(prices.empty())
        return 0;
    vector<vector<int> > dp(prices.size(), vector<int>(3));
    dp[0][0] = -prices[0]; //dp[0][1] = dp[0][2] = 0
    for (int i = 1; i < prices.size();i++){
        dp[i][0] = max(dp[i - 1][2] - prices[i], dp[i - 1][0]); //买了，或者没有买。不可能从冷却期直接到持有
        dp[i][1] = dp[i - 1][0] + prices[i]; //卖了
        dp[i][2] = max(dp[i - 1][1], dp[i - 1][2]); //冷却期过度，或者没有买
    }
    return max(dp[prices.size() - 1][1], dp[prices.size() - 1][2]);
}

时间复杂度：O(n)
空间复杂度：O(n)

  1. 空间优化。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int maxProfit(vector<int>& prices) {
    if(prices.empty())
        return 0;

    int dp0 = -prices[0];
    int dp1 = 0;
    int dp2 = 0;
    for (int i = 1; i < prices.size(); ++i) {
        int dp0_new = max(dp0, dp2 - prices[i]);
        int dp1_new = dp0 + prices[i];
        int dp2_new = max(dp1, dp2);
        dp0 = dp0_new;
        dp1 = dp1_new;
        dp2 = dp2_new;
    }
    return max(dp1, dp2);
}

时间复杂度：O(n)
空间复杂度：O(1)

Leetcode 714. 买卖股票的最佳时机含手续费（中等）

给定一个整数数组 prices，其中第 i 个元素代表了第 i 天的股票价格 ；非负整数 fee 代表了交易股票的手续费用。

你可以无限次地完成交易，但是你每笔交易都需要付手续费。如果你已经购买了一个股票，在卖出它之前你就不能再继续购买股票了。

返回获得利润的最大值。

示例：

1
2
3
4
5
6
7
8
Input: prices = [1, 3, 2, 8, 4, 9], fee = 2  
Output: 8  
Explanation: The maximum profit can be achieved by:  
Buying at prices[0] = 1  
Selling at prices[3] = 8  
Buying at prices[4] = 4  
Selling at prices[5] = 9  
The total profit is ((8 - 1) - 2) + ((9 - 4) - 2) = 8.

题解：

  1. dp。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
int maxProfit(vector<int>& prices, int fee) {
    if (prices.empty())
        return 0;

    int n = prices.size();
    vector<vector<int> > dp(n,vector<int>(2));
    dp[0][0] = 0;
    dp[0][1] = -prices[0];
    for (int i = 1; i < n; i++) {
        dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] + prices[i] - fee);
        dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
    }
    return dp[n - 1][0];
}

时间复杂度：O(n)
空间复杂度：O(n)

  1. 空间优化。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int maxProfit(vector<int>& prices, int fee) {
    if (prices.empty())
        return 0;

    int n = prices.size();
    int dp0 = 0;
    int dp1 = -prices[0];
    for (int i = 1; i < n; i++) {
        int dp0_new = max(dp0, dp1 + prices[i] - fee);
        int dp1_new = max(dp1, dp0 - prices[i]);
        dp0 = dp0_new;
        dp1 = dp1_new;
    }
    return dp0;
}

时间复杂度：O(n)
空间复杂度：O(1)

res

股票问题系列通解

3.2.6 字符串问题

Leetcode 650. 只有两个键的键盘（中等）

最开始只有一个字符 A，问需要多少次操作能够得到 n 个字符 A，每次操作可以复制当前所有的字符，或者粘贴。

示例：

1
2
3
4
5
6
7
输入: 3
输出: 3
解释:
最初, 我们只有一个字符 'A'。
第 1 步, 我们使用 Copy All 操作。
第 2 步, 我们使用 Paste 操作来获得 'AA'。
第 3 步, 我们使用 Paste 操作来获得 'AAA'。

题解：
dp。dp[i]表示通过复制粘贴操作，得到 i 个字符，最少需要几步操作。

如果一个数是素数，那么最少操作就是一开始复制一个，最后一个个粘贴；如果一个数不是素数，那么最少操作就可以按它的因数分解一下，简化操作。

比如12，可以分解为 以下几种情况：

  • 12 = 2*6, 需要操作CPCPPPPP总共8步
  • 12 = 3*4, 需要操作CPPCPPP总共7步
  • 12 = 4*3, 需要操作CPPPCPP总共7步
  • 12 = 6*2, 需要操作CPPPPPCP总共8步

其实可以发现，因子相同的情况下，交换因子相乘的顺序，需要的步骤是一样的。所以我们可以简化一下分解的步骤，只需要找到小于sqrt(n)的因子即可。假设找到的因子是 j ，那么需要的最小步骤就是 dp[j] + dp[i/j]，其中，dp[j]表示需要多少步生成这个因子，dp[i/j]表示需要多少步基于这个因子得到 i。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int minSteps(int n){
    vector<int> dp(n + 1);
    int h = sqrt(n);
    for (int i = 2; i <= n;i++){
        dp[i] = i;
        for (int j = 2; j <= h; j++){
            if(i%j==0){
                dp[i] = dp[j] + dp[i / j];
                break;
            }
        }
    }
    return dp[n];
}

时间复杂度：O(n^(1/2))
空间复杂度：O(1)

3.3 贪心算法(greedy)

每次都选择局部最优的策略，最后达到全局最优。但是，有的问题使用贪心算法不能保证达到全局最优，如 0-1背包问题。

Leetcode 455. 分发饼干（简单）

每个孩子都有一个满足度 grid，每个饼干都有一个大小 size，只有饼干的大小大于等于一个孩子的满足度，该孩子才会获得满足。求解最多可以获得满足的孩子数量。

示例： 

1
2
Input: grid[1,3], size[1,2,4]  
Output: 2

题解：
给一个孩子的饼干应当尽量小并且又能满足该孩子，这样大饼干才能拿来给满足度比较大的孩子。因为满足度最小的孩子最容易得到满足，所以先满足满足度最小的孩子。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int findContentChildren(vector<int>& g, vector<int>& s) {
    sort(g.begin(), g.end());
    sort(s.begin(), s.end());

    int m = g.size();
    int n = s.size();
    int idxG = 0, idxS = 0;
    while(idxG<m && idxS<n){
        if(g[idxG]<=s[idxS])
            idxG++;
        idxS++;
    }
    return idxG;
}

时间复杂度：O(nlogn)，因为要排序
空间复杂度：O(1)

上一题的变体

要求出满足最多孩子的方法中每个孩子得到的的饼干编号。

示例：

1
2
3
输入：grid = {90, 33, 16} size = {9, 20, 50, 40, 99, 1}

输出： 5 4 2

题解：
使用了map的自动key排序功能。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
vector<int> cookiesAssign2(vector<int> &grid, vector<int> &size){
    map<int, int> sizeMap; //key: grid val: idx
    map<int, int> gridMap; //key: size val: idx
    for (int i = 0; i < grid.size(); i++)
        gridMap.insert({grid[i], i});
    
    for (int i = 0; i < size.size();i++)
        sizeMap.insert({size[i], i});

    vector<int> res(grid.size(), -1);
    for (auto itG = gridMap.begin(), itS = sizeMap.begin(); itG != gridMap.end() && itS!=sizeMap.end(); itG++, itS++)
    {
        while(itS!=sizeMap.end() && itS->first < itG->first)
            itS++;
        if(itS==sizeMap.end())
            break;
        res[itG->second] = itS->second;
    }
    return res;
}

Leetcode 435. 无重叠区间（中等）

给定一个区间的集合，找到需要移除区间的最小数量，使剩余区间互不重叠。

示例：

1
2
3
4
5
6
Input: [ [1,2], [1,2], [1,2] ]  
Output: 2  
Explanation: You need to remove two [1,2] to make the rest of intervals non-overlapping.  
Input: [ [1,2], [2,3] ]  
Output: 0  
Explanation: You don't need to remove any of the intervals since they're already non-overlapping.

题解：
先计算最多能组成的不重叠区间个数，然后用区间总个数减去不重叠区间的个数。在每次选择中，区间的结尾最为重要，选择的区间结尾越小，留给后面的区间的空间越大，那么后面能够选择的区间个数也就越大。按区间的结尾进行排序，每次选择结尾最小，并且和前一个区间不重叠的区间。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
bool cmp(const vector<int> &a, const vector<int> &b){
    return a[1] < b[1];
}
int eraseOverlapIntervals(vector<vector<int>>& intervals){
    if(intervals.empty())
        return 0;
    sort(intervals.begin(), intervals.end(), cmp);
    int cnt = 0;
    int end = intervals[0][0];
    for(auto num:intervals){
        if(num[0]>=end){
            cnt++;
            end = num[1];
        }
    }
    return intervals.size()-cnt;
}

时间复杂度：O(nlogn)，因为要排序
空间复杂度：O(1)

Leetcode 452. 用最少数量的箭引爆气球（中等）

气球在一个水平数轴上摆放，可以重叠，飞镖垂直投向坐标轴，使得路径上的气球都被刺破。

示例：

1
2
Input:[[10,16], [2,8], [1,6], [7,12]]  
Output:2

题解：
求解最小的投飞镖次数使所有气球都被刺破。也是计算不重叠的区间个数，不过和 Leetcode 435 的区别在于，[1, 2] 和 [2, 3] 在本题中算是重叠区间。所以if判定条件不要”=”，end初始化要比points[0][0]小。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
bool cmp(const vector<int> &a, const vector<int> &b){
    return a[1] < b[1];
}
int findMinArrowShots(vector<vector<int>>& points) {
    if(points.empty())
        return 0;
    sort(points.begin(), points.end(), cmp);
    int cnt = 0;
    long end = (long)points[0][0]-1;
    for(auto num:points){
        if(num[0]>end){
            cnt++;
            end = num[1];
        }
    }
    return cnt;
}

时间复杂度：O(nlogn)，因为要排序
空间复杂度：O(1)

Leetcode 406. 根据身高重建队列（中等）

乱序重建：一个学生用两个分量 (h, k) 描述，h 表示身高，k 表示排在前面的有 k 个学生的身高比他高或者和他一样高。

示例：

1
2
Input:[[7,0], [4,4], [7,1], [5,0], [6,1], [5,2]]  
Output:[[5,0], [7,0], [5,2], [6,1], [4,4], [7,1]]

题解：
为了使插入操作不影响后续的操作，身高较高的学生应该先做插入操作，否则身高较小的学生原先正确插入的第 k 个位置可能会变成第 k+1 个位置。身高 h 降序、个数 k 值升序，然后将某个学生插入队列的第 k 个位置中。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
bool cmp0aca1dec(const vector<int> &a, const vector<int> &b){
    return a[0] == b[0] ? a[1] <= b[1] : a[0] > b[0];
}
vector<vector<int>> reconstructQueue(vector<vector<int>>& people) {
    if(people.empty())
        return {};
    
    sort(people.begin(), people.end(), cmp0aca1dec);
    
    vector<vector<int> > res;
    for (int i = 0; i < people.size(); i++){
        auto pos = res.begin();
        res.insert(pos+people[i][1], people[i]);
    }
    return res;
}

Leetcode 605. 种花问题（简单）

flowerbed 数组中 1 表示已经种下了花朵。花朵之间至少需要一个单位的间隔，求解是否能种下 n 朵花。

示例：

1
2
Input: flowerbed = [1,0,0,0,1], n = 1  
Output: True

题解： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
bool canPlaceFlowers(vector<int>& flowerbed, int n) {
    int nFlower = flowerbed.size();
    if(n==0)
        return true;
    for (int i = 0; i < nFlower; i++)
    {
        if(flowerbed[i]==1)
            continue;

        int pre = i-1 >= 0 ? flowerbed[i - 1] : 0; //第一个位置?
        int next = i+1 <= nFlower-1 ? flowerbed[i + 1] : flowerbed[nFlower-1];//最后一个位置?
        if(pre==0 && next==0 ){
            flowerbed[i] = 1;
            n--;
        }
        if(n==0)
            return true;
    }
    return false;
}

时间复杂度：O(n)
空间复杂度：O(1)

Leetcode 392.判断子序列（简单）

判断是否为子序列

示例：

1
2
s = "abc", t = "ahbgdc"  
Return true.

题解：
双指针。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
bool isSubsequence(string s, string t) {
    if(t.empty()){
        if(s.empty())
            return true;
        else
            return false;
    }
    
    int idxS=0,idxT=0;
    while(idxS<s.size() && idxT<t.size()){
        if(s[idxS]==t[idxT])
            idxS++;
        idxT++;
    }
    return idxS==s.size();
}

时间复杂度：O(m+n)
空间复杂度：O(1)

Leetcode 665. 非递减数列（简单）

判断一个数组是否能只修改一个数就成为非递减数组。

示例：

1
2
3
Input: [4,2,3]  
Output: True  
Explanation: You could modify the first 4 to 1 to get a non-decreasing array.

题解：
如果下一个点有下降，我们当前点称为拐点，如[1,3,2]中的3。

  • 如果拐点前一个数小于等于拐点后一个数，如[1,3,2,4,5]中1<2，则改变拐点的数，把 3 变成 2 能保证数列不减，且不改变前后的拐点数。
  • 如果拐点前一个数大于拐点后一个数，如[2,3,1,4,5]中2>1，则改变拐点后的数，把 1 变成 3 能保证数列不减，且不改变前后的拐点数。
1
2
3
4
5
6
7
8
9
10
11
12
13
bool checkPossibility(vector<int>& nums) {
    int cnt = 0;
    for (int i = 1; i < nums.size() && cnt < 2;i++){
        if(nums[i]>=nums[i-1])
            continue;
        cnt++;
        if(i>=2 && nums[i-2]>nums[i])
            nums[i] = nums[i - 1];
        else
            nums[i - 1] = nums[i];
    }
    return (cnt <= 1);
}

时间复杂度：O(n)
空间复杂度：O(1)

Leetcode 763. 划分字母区间（中等）

字符串 S 由小写字母组成。我们要把这个字符串划分为尽可能多的片段，同一个字母只会出现在其中的一个片段。返回一个表示每个字符串片段的长度的列表。

示例：

1
2
3
4
5
Input: S = "ababcbacadefegdehijhklij"  
Output: [9,7,8]  
Explanation:  
The partition is "ababcbaca", "defegde", "hijhklij".  
This is a partition so that each letter appears in at most one part. A partition like "ababcbacadefegde", "hijhklij" is incorrect, because it splits S into less parts.

题解：
策略就是不断地选择从最左边起最小的区间。

可以从第一个字母开始分析，假设第一个字母是 ‘a’，那么第一个区间一定包含最后一次出现的 ‘a’。但第一个出现的 ‘a’ 和最后一个出现的 ‘a’ 之间可能还有其他字母，这些字母会让区间变大。举个例子，在 “abccaddbeffe” 字符串中，第一个最小的区间是 “abccaddb”。

通过以上的分析，我们可以得出一个算法：对于遇到的每一个字母，去找这个字母最后一次出现的位置，用来更新当前的最小区间。如果要输出所有子串，把备注取消就可以。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
vector<int> partitionLabels(string S) {
    vector<int> alphabet(26);
    for (int i = 0; i < S.size();i++)
        alphabet[S[i] - 'a'] = i;

    int startIdx = 0, lastIdx = 0;
    //vector<string> subS;
    vector<int> res;
    for (int i = 0; i < S.size(); i++){
        char tmp = S[i];
        lastIdx = max(alphabet[tmp - 'a'], lastIdx);
        if(lastIdx==i){
            res.push_back(lastIdx - startIdx + 1);
            //string tmpStr = S.substr(startIdx, lastIdx - startIdx + 1);
            //subS.push_back(tmpStr);
            startIdx = i + 1;
            lastIdx = i + 1;
        }
    }
    return res;
}

时间复杂度：O(n)
空间复杂度：O(1)

3.4 双指针

双指针主要用于遍历数组，两个指针指向不同的位置，协同完成任务。

（剑指offer的双指针操作）

Leetcode 167. 两数之和 II - 输入有序数组（简单）

给定一个已按照升序排列的有序数组，找到两个数使得它们相加之和等于目标数。

函数应该返回这两个下标值 index1 和 index2，其中 index1 必须小于 index2。

说明:

  • 返回的下标值（index1 和 index2）不是从零开始的。
  • 你可以假设每个输入只对应唯一的答案，而且你不可以重复使用相同的元素。

示例：

1
2
Input: numbers={2, 7, 11, 15}, target=9  
Output: index1=1, index2=2

题解：

  1. 使用双指针，一个指针指向值较小的元素，一个指针指向值较大的元素。指向较小元素的指针从头向尾遍历，指向较大元素的指针从尾向头遍历：
  • 如果两个指针指向元素的和 sum == target，那么得到要求的结果；
  • 如果 sum > target，移动较大的元素，使 sum 变小一些；
  • 如果 sum < target，移动较小的元素，使 sum 变大一些。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
vector<int> twoSum(vector<int>& numbers, int target) {
    if(numbers.empty())
        return {};
    int start = 0;
    int end = numbers.size()-1;
    while(start<end){
        if(numbers[start]+numbers[end] == target)
            return {start+1, end+1};
        if(numbers[start]+numbers[end]>target)
            end --;
        else if(numbers[start]+numbers[end]<target)
            start ++;
    }
    return {};
}

时间复杂度：O(n)
空间复杂度：O(1)

  1. 哈希表。无序的序列也适用。
1
2
3
4
5
6
7
8
9
10
11
12
vector<int> twoSum(vector<int>& numbers, int target) {
    unordered_map<int, int> numMap;
    for (int i = 0; i < numbers.size();i++)
        numMap[numbers[i]] = i;

    for (int i = 0; i < numbers.size();i++){
        auto it = numMap.find(target - numbers[i]);
        if (it != numMap.end())
            return {i + 1, it->second+1};
    }
    return {};
}

时间复杂度：O(n)
空间复杂度：O(n)

Leetcode 633. 平方数之和（简单）

给定一个非负整数 c ，你要判断是否存在两个整数 a 和 b，使得 a2 + b2 = c 。

示例：

1
2
3
Input: 5  
Output: True  
Explanation: 1 * 1 + 2 * 2 = 5

题解：
本题和 「167. 两数之和 II - 输入有序数组」 类似，只有一个明显区别：一个是和为 target，一个是平方和为 target。本题同样可以使用双指针得到两个数，使其平方和为 target。
本题的关键是右指针的初始化，实现剪枝，从而降低时间复杂度。设右指针为 x，左指针固定为 0，为了使 0^2 + x^2 的值尽可能接近 target，我们可以将 x 取为 sqrt(target)。因为最多只需要遍历一次 0-sqrt(target)，所以时间复杂度为 O(sqrt(target))。又因为只使用了两个额外的变量，因此空间复杂度为 O(1)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
bool judgeSquareSum(int c) {
    if(c < 0) 
        return false;
    int start = 0;
    int end = sqrt(c);
    while(start<=end){
        if((long)start*start + (long)end*end == (long)c)
            return true;
        else if((long)start*start + (long)end*end > (long)c)
            end--;
        else
            start++;
    }
    return false;
}

时间复杂度：O(c^(1/2))
空间复杂度：O(1)

Leetcode 345. 反转字符串中的元音字母（简单）

反转字符串中的元音字符

示例：

1
Given s = "Leetcode", return "Leotcede".

题解：
使用双指针，一个指针从头向尾遍历，一个指针从尾到头遍历，当两个指针都遍历到元音字符时，交换这两个元音字符。为了快速判断一个字符是不是元音字符，我们将全部元音字符添加到集合 HashSet 中，从而以 O(1) 的时间复杂度进行该操作。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
string reverseVowels(string s) {
    unordered_set<char> hs = {'a','e','i','o','u','A','E','I','O','U'};//c++11之后才可以这样初始化
    int start = 0;
    int end = s.size() - 1;
    string res = s;
    while (start<end)
    {
        char tmp_start = s[start];
        char tmp_end = s[end];
        if (hs.find(tmp_start)==hs.end())//tmp不在hs中
            res[start++] = tmp_start;
        else if(hs.find(tmp_end)==hs.end())
            res[end--] = tmp_end;
        else{
            res[start++] = tmp_end;
            res[end--] = tmp_start;
        }
    }
    return res;
}

时间复杂度：O(n)
空间复杂度：O(1)

Leetcode 680. 验证回文字符串 Ⅱ（简单）

给定一个非空字符串 s，最多删除一个字符。判断是否能成为回文字符串。

示例：

1
2
3
Input: "abca"  
Output: True  
Explanation: You could delete the character 'c'.

题解：
使用双指针可以很容易判断一个字符串是否是回文字符串：
令一个指针从左到右遍历，一个指针从右到左遍历，这两个指针同时移动一个位置，每次都判断两个指针指向的字符是否相同，如果都相同，字符串才是具有左右对称性质的回文字符串。在判断是否为回文字符串时，我们不需要判断整个字符串，因为左指针左边和右指针右边的字符之前已经判断过具有对称性质，所以只需要判断中间的子字符串即可。在试着删除字符时，我们既可以删除左指针指向的字符，也可以删除右指针指向的字符。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
bool isPalindrome(string s,int start,int end){
    while(start < end){
        if (s[start++]!=s[end--])
            return false;
    }
    return true;
}
bool validPalindrome(string s) {
    if(s.size()<=1)
        return true;
    int start = 0;
    int end = s.size() - 1;
    bool res = true;
    while (start < end)
    {
        if (s[start] != s[end])
        {
            res = isPalindrome(s, start + 1, end) || isPalindrome(s, start, end - 1);
            return res;
        }
        start++;
        end--;
    }
    return res;
}

时间复杂度：O(n)
空间复杂度：O(1)

Leetcode 88. 合并两个有序数组（简单）

归并两个有序数组，把归并结果存到第一个数组上。

示例：

1
2
3
4
Input:  
nums1 = [1,2,3,0,0,0], m = 3  
nums2 = [2,5,6],       n = 3  
Output: [1,2,2,3,5,6]

题解：
需要从尾开始遍历，否则在 nums1 上归并得到的值会覆盖还未进行归并比较的值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
    int idx1 = m - 1;
    int idx2 = n - 1;
    int idx = m + n - 1;
    while (idx1>=0 || idx2>=0){
        if(idx1<0)
            nums1[idx--] = nums2[idx2--];
        else if(idx2<0)//这时候nums2已经插完，其实可以直接return nums1了
            nums1[idx--] = nums1[idx1--];
        else if(nums1[idx1]>nums2[idx2])
            nums1[idx--] = nums1[idx1--];
        else
            nums1[idx--] = nums2[idx2--];
    }
}

时间复杂度：O(m+n)
空间复杂度：O(1)

Leetcode 141. 环形链表（简单）

判断链表是否存在环

  1. 双指针（快慢指针），一个指针每次移动一个节点，一个指针每次移动两个节点，如果存在环，那么这两个指针一定会相遇。
1
2
3
4
5
6
7
8
9
10
11
12
13
bool hasCycle(ListNode *head) {
    if(head == nullptr || head->next == nullptr)
        return false;
    ListNode *p1 = head->next;
    ListNode *p2 = head->next->next;
    while(p2!=nullptr && p2->next!=nullptr){
        if(p1->val == p2->val)
            return true;
        p1 = p1->next;
        p2 = p2->next->next;
    }
    return false;
}

时间复杂度：O(n)
空间复杂度：O(1)

  1. 哈希表。
1
2
3
4
5
6
7
8
9
10
11
12
bool hasCycle(ListNode *head) {
    if(head == nullptr || head->next == nullptr)
        return false;
    unordered_set<ListNode *> us;
    while (head != nullptr){
        if (us.count(head))
            return true;
        us.insert(head);
        head = head->next;
    }
    return false;
}

时间复杂度：O(n)
空间复杂度：O(n)

Leetcode 524. 通过删除字母匹配到字典里最长单词（中等）

给定一个字符串和一个字符串字典，找到字典里面最长的字符串，该字符串可以通过删除给定字符串的某些字符来得到。如果答案不止一个，返回长度最长且字典顺序最小的字符串。如果答案不存在，则返回空字符串。

示例：

1
2
Input: s = "abpcplea", d = ["ale","apple","monkey","plea"]  
Output: "apple"

题解：
可以使用双指针来判断一个字符串是否为另一个字符串的子序列。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
bool isSubstr(string s, string d){
    int i = 0;
    int j = 0;
    while(i<s.size() && j<d.size()){
        if(s[i]==d[j]){
            j++;
        }
        i++;
    }
    return j == d.size();
}
string findLongestWord(string s, vector<string>& d) {
    string res = "";
    for (string cur:d){
        if(res.size()>cur.size() || (res.size()==cur.size() && res<cur))
            continue;
        if (isSubstr(s, cur))
            res = cur;
    }
    return res;
}

时间复杂度：O(nl)，l 是字典里字符串的平均长度
空间复杂度：O(n)

Leetcode 75. 颜色分类（中等）

给定一个包含红色、白色和蓝色，一共 n 个元素的数组，原地对它们进行排序，使得相同颜色的元素相邻，并按照红色、白色、蓝色顺序排列。

此题中，我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。

示例：

1
2
Input: [2,0,2,1,1,0] 
Output: [0,0,1,1,2,2]

题解： 

1
2
3
4
5
6
7
8
9
10
11
12
13
void sortColors(vector<int>& nums) {
    int zero = -1;
    int one = 0;
    int two = nums.size();
    while(one<two){
        if(nums[one]==0)
            swap(nums[++zero],nums[one++]);
        else if(nums[one]==2)
            swap(nums[--two], nums[one]); //从后面换上来的可能是0，所以one不能往后移动
        else
            one++;
    }
}

时间复杂度：O(n)
空间复杂度：O(1)

Leetcode 42. 接雨水（困难）

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例：

1
2
输入: [0,1,0,2,1,0,1,3,2,1,2,1]
输出: 6

题解：

  1. 用left_max[i] 和 right_max[i] 表示 i 左边和右边的最大值。这样就把暴力法时间复杂度的O(n^2)降为O(n)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
int trap(vector<int>& height)
{
    if (height.empty())
        return 0;
    int res = 0;
    int n = height.size();
    vector<int> left_max(n), right_max(n);
    left_max[0] = height[0];
    for (int i = 1; i < n; i++) {
        left_max[i] = max(height[i], left_max[i - 1]);
    }
    right_max[n - 1] = height[n - 1];
    for (int i = n - 2; i >= 0; i--) {
        right_max[i] = max(height[i], right_max[i + 1]);
    }
    for (int i = 1; i < n - 1; i++) {
        res += min(left_max[i], right_max[i]) - height[i];
    }
    return res;
}

时间复杂度：O(n)
空间复杂度：O(n)

  1. 双指针。
    算法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int trap(vector<int>& height)
{
    int left = 0, right = height.size() - 1;
    int res = 0;
    int left_max = 0, right_max = 0;
    while (left < right) {
        if (height[left] < height[right]) {
            height[left] >= left_max ? (left_max = height[left]) : res += (left_max - height[left]);
            left++;
        }
        else {
            height[right] >= right_max ? (right_max = height[right]) : res += (right_max - height[right]);
            right--;
        }
    }
    return res;
}

时间复杂度：O(n)
空间复杂度：O(1)

3.5 排序（Sorting）

python实现的八大排序

cpp实现八大排序：

  • 插入排序

  • 希尔排序

  • 选择排序

  • 冒泡排序

  • 快速排序

  • 堆排序

  • 归并排序

  • 基数排序

  • 快排变为稳定排序的方法。三遍扫描原序列：

    1. 第一遍先把小于pivot的元素按先后顺序放到tmp里，然后把pivot放到它的正确位置tmp[k]；
    2. 第二遍把大于pivot的元素按先后顺序追加在tmp里，这样除了pivot以前的其他元素，都保持了和原序列中一样的顺序；
    3. 第三遍把tmp赋值回原数组A。

3.5.1 Partition函数

Partition函数可以用在快排中，也可以用来实现在长度为n的数组中查找第k大的数字。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
int Partition(std::vector<int> &nums, int start, int end)
{
    if (nums.size() < 2 || start<0 || end>nums.size())
        return -1;

    int idx = start + std::rand() % (end - start + 1);//随机生成一个[start,end]的整数
    int pivot = nums[idx];
    nums[idx] = nums[start];//相当于把nums[idx]换到首位
    while (start < end) {
        while (start < end && nums[end] >= pivot)
            end--;
        nums[start] = nums[end];
        while (start < end && nums[start] <= pivot)
            start++;
        nums[end] = nums[start];
    }
    nums[start] = pivot;
    return start;
}

快排（cpp）

递归版

1
2
3
4
5
6
7
8
9
void QuickSort(vector<int> &arr, int start, int end){
    if(start==end)
        return;
    int mid = Partition(arr, start, end);
    if(mid>start)
        QuickSort(arr, start, mid - 1);
    if(mid<end)
        QuickSort(arr, mid + 1, end);
}

非递归版

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
void QuickSort(vector<int> &nums){
    if (nums.empty())
        return;
    stack<int> stk;
    stk.push(nums.size()-1);//先压右指针
    stk.push(0);//再压左指针
    while (!stk.empty()){
        int start = stk.top();//先弹出左指针
        stk.pop();
        int end = stk.top();//再弹出右指针
        stk.pop();
        if (start < end){
            int mid = Partition(nums, start, end);
            if (mid > start){//保存中间变量
                stk.push(mid - 1);
                stk.push(start);  
            }
            if (end > mid){
                stk.push(end);
                stk.push(mid + 1);
            }
        }
    }
}

3.5.2 例题

TOP K 问题

  • 排序 ：时间复杂度 O(NlogN)，空间复杂度 O(1)
  • 堆 ：时间复杂度 O(NlogK)，空间复杂度 O(K)
  • 快速选择 ：时间复杂度 O(N)，空间复杂度 O(1)
Leetcode 215. 数组中的第K个最大元素（中等）

在未排序的数组中找到第 k 个最大的元素。请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。

示例：

1
2
3
Input: [3,2,1,5,6,4] and k = 2  
Output: 5  
Kth Element, 在排序数组中 == 找到倒数第 k 个的元素。

题解：

  1. 快排变形。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int findKthLargest(vector<int>& nums, int k) {
    int target = nums.size()-k;
    int l = 0;
    int r = nums.size()-1;
    while(l<r){
        int m = Partition(nums,l,r);
        if(m==target)
            return nums[m];
        else if(m<target)
            l = m+1;
        else
            r = m-1;
    }
    return nums[l];
}

时间复杂度：O(n)
空间复杂度：O(logn)，递归的栈深度

  1. 堆
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
void adjustHeap(std::vector<int> &nums, int parents, int end)
{
    //非叶子结点parents的两个子节点（假设都存在）
    int lchild = 2 * parents + 1;
    int rchild = 2 * parents + 2;
    int maxIdx = parents;
    if (lchild <= end && nums[maxIdx] < nums[lchild]) 
        maxIdx = lchild;
    if (rchild <= end && nums[maxIdx] < nums[rchild])
        maxIdx = rchild;
    if (maxIdx != parents) {
        swap(nums[parents],nums[maxIdx]);
        //交换之后，nums[maxIdx]应该是较小的元素，所以应该向下继续调整
        adjustHeap(nums, maxIdx, end);
    }
}

void buildHeap(std::vector<int> &nums)
{//建堆
    for (int i = nums.size() / 2 - 1; i >= 0; i--) {
        //从倒数第一个非叶子结点开始调整
        adjustHeap(nums, i, nums.size() - 1);
    }
}

int findKthLargest(vector<int>& nums, int k) {
    int end = nums.size()-1;
    buildHeap(nums);
    for (int i = nums.size() - 1; i >= nums.size() - k + 1; i--) {
        swap(nums[0], nums[i]);
        end--;
        adjustHeap(nums, 0, end);
    }
    return nums[0];
}

时间复杂度：O(nlogn)，建堆的时间代价是 O(n)，删除的总代价是 O(klogn)。因为k < n，所以是O(nlogn)
空间复杂度：O(logn)

BFPRT

也可以用BFPRT算法，具体实现如下。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
int BFPRT(vector<int> &nums, int start, int end, int k); //因为findMidIdx与BFPRT互相调用，所以最好在前面声明
int findMidIdx(vector<int> &nums, int start, int end);

int selectSort(vector<int> &nums,int start,int end)
{//选择排序，返回中位数下标
    int temp;
    for (int i = start; i < end; i++){
        for (int j = i + 1; j <= end; j++)
        {
            if (nums[i] > nums[j])
                swap(nums[i], nums[j]);
        }
    }
    return (((end - start) / 2) + start);
}

int findMidIdx(vector<int> &nums,int start,int end)
{//返回中位数的中位数下标
    if (end - start < 5)
        return (selectSort(nums, start, end));//插入排序也可以

    int subRIdx = start - 1;
    for (int i = start; i + 4 <= end; i += 5)
    {
        int index = selectSort(nums, i, i + 4); //找到五个元素的中位数的下标
        swap(nums[++subRIdx], nums[index]);   //依次放在左侧
    }

    return BFPRT(nums, start, subRIdx, ((subRIdx - start + 1) / 2) + 1);
}

int Partition(vector<int> &nums,int start,int end,int pivotIdx)
{
    swap(nums[pivotIdx], nums[end]);

    int divideIdx = start;
    for (int i = start; i < end; i++)
    {
        if (nums[i]<nums[end])
            swap(nums[divideIdx++], nums[i]);
    }

    swap(nums[divideIdx], nums[end]);
    return divideIdx;
}

int BFPRT(vector<int> &nums, int start,int end,int k)
{
    /*
    求第k小，返回其位置的下标。
    如果求TOP K，改变大小于符号，或者返回 n-K+1
    */
    int pivotIdx = findMidIdx(nums, start, end); //得到中位数的中位数下标
    int divideIdx = Partition(nums, start, end, pivotIdx); //进行划分，返回划分边界
    int n = divideIdx - start + 1;
    if (n == k)
        return divideIdx;
    else if (n > k)
        return BFPRT(nums, start, divideIdx - 1, k);
    else
        return BFPRT(nums, divideIdx + 1, end, k - n);
}

Leetcode 347. 前 K 个高频元素（中等）

给定一个非空的整数数组，返回其中出现频率前 k 高的元素。

示例：

1
Given [1,1,1,2,2,3] and k = 2, return [1,2].

Leetcode提交的答案：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class cmp{
public:
    bool operator()(const pair<int, int> &a, const pair<int, int> &b){
        return a.second > b.second;
    }
};

vector<int> topKFrequent(vector<int> &nums, int k){
    map<int, int> numMap;
    for(int n:nums)
        numMap[n]++;

    priority_queue<pair<int, int>,vector<pair<int,int> >, cmp > pq;
    for (auto it = numMap.begin(); it != numMap.end(); it++){
        pq.push(*it);
        if(pq.size()>k)
            pq.pop();
    }
    vector<int> res(k);
    for (int i = k - 1; i >= 0; i--) {
        res[i] = pq.top().first;
        pq.pop();
    }
    return res;
}

小根堆：

  • 遍历数组，哈希表录入频率
  • 遍历哈希表，维护一个出现频率前k多的小根堆
  • 优先队列已满，需要判断当前元素的频率是否大于优先队列的最小频率元素的频率，如果大于，则替换。
  • 优先队列未满，进队即可

桶：
设置若干个桶，每个桶存储出现频率相同的数。桶的下标表示数出现的频率，即第 i 个桶中存储的数出现的频率为 i。把数都放到桶之后，从后向前遍历桶，最先得到的 k 个数就是出现频率最多的的 k 个数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
void topKFrequent(){
//小根堆
    vector<int> nums = {1, 1, 1, 2, 2, 3};
    int k = 2;
    //map里面是（元素，频率）
    unordered_map<int,int> freq;
    for (int i = 0; i < nums.size();i++){
        freq[nums[i]]++; //可以验证，freq[nums[i]]初始化为0哦
    }
    //优先队列中，按频率排序，所以数据对是(频率，元素)形式
    priority_queue<pair<int, int>, vector<pair<int, int> >, greater<pair<int, int> > > pq;
    for (auto it = freq.begin(); it != freq.end();it++){
        if(pq.size()==k){//队列满了
            if(pq.top().first < it->second){
                pq.pop();
                pq.push(make_pair(it->second,it->first));
            }
        }
        else{
            pq.push(make_pair(it->second, it->first));
        }
    }
    vector<int> result;
    while(!pq.empty()){
        result.push_back(pq.top().second);
        // cout << pq.top().second << endl;
        pq.pop();
    }  
//桶
    int n = nums.size()+1;
    vector< vector<int> > buckets(n);
    for (auto it = freq.begin(); it != freq.end(); it++)
    {
        buckets[it->second].push_back(it->first);
    }
    vector<int> topK;
    for (int i = buckets.size() - 1; i > 0 && topK.size()<k; i--){
        if(buckets[i].size()==0)
            continue;
        for (int j = 0; j < buckets[i].size() && topK.size() < k;j++){
            topK.push_back(buckets[i].back());
            buckets[i].pop_back();
        }
    }
}

Leetcode 451. 根据字符出现频率排序（中等）

给定一个字符串，请将字符串里的字符按照出现的频率降序排列。

示例1：

1
2
3
4
5
6
7
8
9
输入:
"cccaaa"

输出:
"cccaaa"

解释:
'c'和'a'都出现三次。此外，"aaaccc"也是有效的答案。
注意"cacaca"是不正确的，因为相同的字母必须放在一起。

示例2:

1
2
3
4
5
6
7
8
9
输入:
"Aabb"

输出:
"bbAa"

解释:
此外，"bbaA"也是一个有效的答案，但"Aabb"是不正确的。
注意'A'和'a'被认为是两种不同的字符。

题解：

  1. 桶。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
string frequencySort(string s) {
    unordered_map<char, int> freq;
    for (int i = 0; i < s.size();i++)
        freq[s[i]]++;
    //桶
    int n = s.size();
    vector<vector<char> > buckets(n + 1);
    for (auto it = freq.begin(); it != freq.end();it++){
        buckets[it->second].push_back(it->first);
    }
    string res = "";
    for (int i = buckets.size() - 1; i > 0; i--)
    {
        if(buckets[i].size()==0)
            continue;
        for(auto s : buckets[i]){
            for (int j = 0; j < i; j++)
                res += s;
        }
    }
    return res;
}

时间复杂度：O(n)
空间复杂度：O(n)

  1. 堆。方法同Leetcode 347。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
string frequencySort(string s) {
    unordered_map<char, int> ump;
    for (char &c : s)
        ump[c]++;
    
    priority_queue<pair<int, char>> pq;
    for (auto &m : ump)
        pq.push({m.second, m.first});

    string res;
    while (!pq.empty()) {
        auto tmp = pq.top(); 
        pq.pop();
        res.append(tmp.first, tmp.second);
    }
    return res;
}

时间复杂度：O(n)
空间复杂度：O(k)，k为不同字母的数量，最大为26

范围排序

给一个无序不重复的数组nums，两个整数int a和int b，其中a <= b <= nums.size()-1。返回第a到第b个排序子数组。

示例：

1
2
3
nums = {3,5,4,1,2}, a = 2, b = 4

输出：[2,3,4]

题解：
快排的变形。Partition找位置i，再根据i与a、b的比较来递归往下排序。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
//Partition函数在上面

void quickSort(vector<int> &nums, int start, int end, int a, int b){
    if(start > end)
        return;
    int mid = Partition(nums, start, end);
    if(mid>=b-1)
        quickSort(nums, start, mid - 1, a, b);
    if(mid<=a-1)
        quickSort(nums, mid + 1, end, a, b);
    if(mid>a-1 && mid<b-1){
        quickSort(nums, start, mid - 1, a, b);
        quickSort(nums, mid + 1, end, a, b);
    }
}

vector<int> getVec(vector<int> &nums, int a, int b){
    quickSort(nums, 0, nums.size() - 1, a, b);

    vector<int> res;
    for (int i = a-1; i <= b-1; i++)
        res.push_back(nums[i]);

    return res;
}

特殊规则排序

有一种排序算法：每次只能把一个元素提到数组的开头。输入一个乱序数组，输出最少需要多少次操作才能是数组升序排列。

示例：

1
2
3
4
5
输入： [2,1,3,4]

输出： 1

解释：把 1 提到开头就能满足要求

题解：
只需求有多少个数已经按升序的顺序位于数组中就可以了。

1
2
3
4
5
6
7
8
9
10
11
12
13
int timesToAsc(vector<int> &nums){
    vector<int> finalNum = nums;
    sort(finalNum.begin(), finalNum.end());
    int i, j , cnt = 0;
    i = j = nums.size() - 1;
    for (; i >= 0;i--){
        if(finalNum[j] == nums[i]){
            j--;
            cnt++;
        }
    }
    return nums.size() - cnt;
}

3.6 查找/搜索（Search）

3.6.1 回溯算法（backtracking）

回溯法框架

1
2
3
4
5
6
7
8
9
result = []
def backtrack(路径, 选择列表):
    if 满足结束条件:
        result.add(路径)
        return
    for 选择 in 选择列表:
        做选择
        backtrack(路径, 选择列表)
        撤销选择

Leetcode 17. 电话号码的字母组合（中等）

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。

给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

示例：

1
2
Input: "23"  
Output: ["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"].

题解：

  1. 回溯。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
map<char, string> keys = {
    {'2', "abc"}, {'3', "def"}, {'4', "ghi"}, {'5', "jkl"}, {'6', "mno"},
    {'7', "pqrs"}, {'8', "tuv"}, {'9', "wxyz"}
};
void backtracking(string preStr, vector<string> &combinations, const string &digits){
    if(preStr.size()==digits.size()){
        combinations.push_back(preStr);
        return;
    }
    int curIdx = preStr.size();
    char curDigital = digits[curIdx];
    string curKeys = keys[curDigital];
    for(char &k : curKeys){
        preStr += k;
        backtracking(preStr,combinations,digits);
        preStr.erase(preStr.size()-1);
    }
}
vector<string> letterCombinations(string digits) {
    if(digits.empty())
        return {};
    vector<string> res;
    backtracking("", res, digits);
    return res;
}

时间复杂度：O(3^m * 4^n)，其中 m 是输入中对应 3 个字母的数字个数（包括数字 2、3、4、5、6、8），n 是输入中对应 4 个字母的数字个数（包括数字 7、9），m+n 是输入数字的总个数。
空间复杂度：O(m+n)

  1. 队列
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    map<char, string> keys = {
        {'2', "abc"}, {'3', "def"}, {'4', "ghi"}, {'5', "jkl"}, {'6', "mno"},
        {'7', "pqrs"}, {'8', "tuv"}, {'9', "wxyz"}
    };

    vector<string> letterCombinations(string digits) {
        queue<string> que;
        for (int idx = 0; idx < digits.size();idx++)
        {
            char s = digits[idx];
            string key = keys[s];
            if(que.empty()){
                for(auto k:key){
                    string tmp(1, k);
                    que.push(tmp);
                }
            }else{
                while(que.front().size()<=idx){
                    string preStr = que.front();
                    que.pop();
                    for(auto k:key)
                        que.push(preStr + k);
                }
            }
        }
        vector<string> res;
        while (!que.empty()){
            res.push_back(que.front());
            que.pop();
        }
        return res;
    }

Leetcode 93. 复原IP地址（中等）

给定一个只包含数字的字符串，复原它并返回所有可能的 IP 地址格式。

有效的 IP 地址 正好由四个整数（每个整数位于 0 到 255 之间组成，且不能含有前导 0），整数之间用 ‘.’ 分隔。

示例：

1
2
Given "25525511135",  
return ["255.255.11.135", "255.255.111.35"].

题解：
回溯。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
void backtracking(int k, string preIp, string resStr, vector<string> &addresses){
    if(k==4 || resStr.size()==0){
        if(k==4 && resStr.size()==0)
            addresses.push_back(preIp);
        return;
    }
    for (int i = 0; i < resStr.size() && i < 3;i++){
        if(i!=0 && resStr[0]=='0')
            break;
        string part = resStr.substr(0, i + 1);
        if(stoi(part)<=255){
            if(preIp.size()!=0)
                part = '.' + part;
            preIp = preIp + part;
            backtracking(k + 1, preIp, resStr.substr(i + 1), addresses);
            preIp = preIp.erase(preIp.size() - part.size());
        }
    }
}
vector<string> restoreIpAddresses(string s) {
    vector<string> res;
    backtracking(0, "", s, res);
    return res;
}

huawei 真题

求最大递归调用链栈总和

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
vector<vector<int> > inputStack = {
                                    {5,2,3,1,0,0},
                                    {1,20,2,3},
                                    {2,30,3,4,5},
                                    {3,50,4},
                                    {4,60},
                                    {5,80}
                                  };
void backtracking(int fun, vector<bool> &isHead, bool &isRecursive, vector<bool> &hasVisited, vector<int> &preChain, vector<vector<int> > &callChains){
    if(isRecursive)
        return;
    if (inputStack[0][fun] == 0)
    {
        callChains.push_back(preChain);
        return;
    }
    for (int i = 2; i < inputStack[fun].size();i++){
        int nextFun = inputStack[fun][i];
        if(hasVisited[nextFun]){
            isRecursive = true;
            return;
        }
        isHead[nextFun] = false;
        hasVisited[nextFun] = true;
        preChain.push_back(nextFun);
        backtracking(nextFun, isHead, isRecursive, hasVisited, preChain, callChains);
        preChain.pop_back();
        hasVisited[nextFun] = false;
    }
}
void maxStack(){
    vector<vector<int> > callChains;
    vector<int> preChain;
    vector<bool> isHead(inputStack[0][0]+1,true);
    bool isRecursive = false; //注意！ 如果这个变量不是放在main函数前的全局变量，递归函数传值就必须传引用，不然会因为函数参数传值的复制造成递归的时候不能改变
    for (int i = 1; i <= inputStack[0][0]; i++)
    {
        if(isHead[i]){
            vector<bool> hasVisited(inputStack[0][0] + 1, false);
            preChain.push_back(i);
            hasVisited[i] = true;
            backtracking(i, isHead, isRecursive, hasVisited, preChain, callChains);
        }
    }
    if(isRecursive)
        cout << 'R' << endl;
    else{
        for (auto cc : callChains)
        {
            for(int c:cc)
                cout << c << " ";
            cout << endl;
        }
    }
}

Leetcode 46. 全排列（中等）

给定一个 没有重复 数字的序列，返回其所有可能的全排列。

示例：

1
2
3
4
5
6
7
8
[1,2,3] have the following permutations:  

[ [1,2,3],  
  [1,3,2],  
  [2,1,3],  
  [2,3,1],  
  [3,1,2],  
  [3,2,1] ]

题解：
回溯。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
void backtracking(vector<int> &resNums, vector<int> &preNum, vector<vector<int> > &permuteList){
    if(resNums.size()==0){
        permuteList.push_back(preNum);
        return;
    }
    for (int i = 0; i < resNums.size();i++){
        int curNum = resNums[i];
        auto it = resNums.begin();
        resNums.erase(it + i);
        preNum.push_back(curNum);
        backtracking(resNums, preNum, permuteList);
        preNum.pop_back();
        resNums.insert(it + i, curNum);
    }
}
vector<vector<int>> permute(vector<int>& nums) {
    vector<vector<int> > res;
    vector<int> preNum;
    backtracking(nums, preNum, res);
    return res;
}

时间复杂度：O(n*n!)
空间复杂度：O(n)

Leetcode 77. 组合（中等）

给定两个整数 n 和 k，返回 1 … n 中所有可能的 k 个数的组合。

示例：

1
2
3
4
5
6
7
8
If n = 4 and k = 2, a solution is:
[ 
  [2,4],  
  [3,4],  
  [2,3],  
  [1,2],  
  [1,3],  
  [1,4], ]

题解： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
void combinationsCore(int n, int k, int start, vector<int> &preRes, vector<vector<int> > &res){
    if(preRes.size()==k){
        res.push_back(preRes);
        return;
    }
    for (int i = start; i <= n; i++)
    {
        preRes.push_back(i);
        combinationsCore(n, k, i + 1, preRes, res);
        preRes.pop_back();
    }
}
vector<vector<int>> combine(int n, int k) {
    vector<vector<int> > res;
    vector<int> preRes;
    combinationsCore(n, k, 1, preRes, res);
    return res;
}

Leetcode 39.组合总和（中等）

给定一个无重复元素的数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的数字可以无限制重复被选取。

示例：

1
2
given candidate set [2, 3, 6, 7] and target 7, A solution set is:  
[ [7],[2, 2, 3] ]

题解：
回溯。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
void backtracking(int target, vector<int> &preCombination, int start, vector<vector<int> > &combination, vector<int> &candidates){
    if(target==0){
        combination.push_back(preCombination);
        return;
    }
    for (int i = start; i < candidates.size();i++)
    {
        int curNum = candidates[i];
        if (target >= curNum)
        {
            preCombination.push_back(curNum);
            backtracking(target - curNum, preCombination, i, combination, candidates);
            preCombination.pop_back();
        }
    }
}
vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
    vector<vector<int> > res;
    vector<int> preCombination;
    backtracking(target, preCombination, 0, res, candidates);
    return res;
}

Leetcode 40. 组合总和 II（中等）

给定一个数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用一次。

示例：

1
2
3
4
5
6
For example, given candidate set [10, 1, 2, 7, 6, 1, 5] and target 8,
A solution set is:  
[ [1, 7],  
[1, 2, 5],  
[2, 6],  
[1, 1, 6]  ]

题解：
回溯

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
void backtracking(int target, vector<int> &preCombination, int start, vector<vector<int> > &res, vector<int> &candidates){
    if(target==0){
        auto it = find(res.begin(), res.end(), preCombination);
        if(it==res.end()){//因为candidates中有重复元素，会导致重复的解，所以查找是否有重复解，没有再放到解集中
            res.push_back(preCombination);
            return;
        }
    }
    for (int i = start; i < candidates.size();i++){
        int curNum = candidates[i];
        if(curNum<=target){
            preCombination.push_back(curNum);
            backtracking(target - curNum, preCombination, i + 1, res, candidates);
            preCombination.pop_back();
        }
    }
}
vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
    sort(candidates.begin(),candidates.end());//先排序才好查重复解
    vector<vector<int>> res;
    vector<int> preCombination;
    vector<bool> hasVisited(candidates.size(),false);
    backtracking(target, preCombination, 0, res, candidates);
    return res;
}

Leetcode 216. 组合总和 III（中等）

找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数，并且每种组合中不存在重复的数字。

示例：

1
2
3
4
Input: k = 3, n = 9  
Output:  
[[1,2,6], [1,3,5], [2,3,4]]  
从 1-9 数字中选出 k 个数不重复的数，使得它们的和为 n。

题解： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
void backtracking(int k, int target, int start, vector<int> &preCombination, vector<vector<int> > &res){
    // if(target<0)
    //     return;
    if (target == 0 && k == 0)
    {
        res.push_back(preCombination);
        return;
    }
    if(target==0 || k==0)
        return;
    for (int i = start; i <= 9;i++){
        if(target<i)//后面的都大于target，不用再往后找了。如果上面用了target<0的判断，这里可以不用，但是下面的调用次数会多一些
            break;
        preCombination.push_back(i);
        backtracking(k - 1, target - i, i+1, preCombination, res);
        preCombination.pop_back();
    }
}
vector<vector<int>> combinationSum3(int k, int n) {
    vector<vector<int> > res;
    vector<int> preCombination;
    backtracking(k, n, 1, preCombination, res);
    return res;
}

Leetcode 78. 子集（中等）

给定一组不含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。

说明：解集不能包含重复的子集。

示例：

1
2
3
4
5
6
7
8
9
10
11
找出集合的所有子集，子集不能重复，[1, 2] 和 [2, 1] 这种子集算重复  
输入: nums = [1,2,3]  
输出:  
[ [3],  
  [1],  
  [2],  
  [1,2,3],  
  [1,3],  
  [2,3],  
  [1,2],  
  []  ]

题解：
回溯。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
void backtracking(int start, int size, vector<int> &preSet, vector<vector<int> > &res, vector<int> &nums){
    if(preSet.size()==size){
        res.push_back(preSet);
        return;
    }
    for (int i = start; i < nums.size();i++){
        preSet.push_back(nums[i]);
        backtracking(i + 1, size, preSet, res, nums);
        preSet.pop_back();
    }
}
vector<vector<int>> subsets(vector<int>& nums) {
    vector<int> preSet;
    vector<vector<int> > res;
    for (int size = 0; size <= nums.size();size++)//子集的大小
        backtracking(0, size, preSet, res, nums); 
    return res;
}

Leetcode 90. 子集 II（中等）

给定一个可能包含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。

说明：解集不能包含重复的子集。

示例：

1
2
3
4
5
6
7
8
输入: [1,2,2]  
输出:  
[   [2],
    [1],
    [1,2,2],
    [2,2],
    [1,2],
    [] ]

题解：
回溯。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
void backtracking(int start, int size, vector<int> &preSet, vector<vector<int> > &res, vector<int> &nums){
    if(preSet.size()==size){
        res.push_back(preSet);
        return;
    }
    for (int i = start; i < nums.size();i++){
        preSet.push_back(nums[i]);
        backtracking(i + 1, size, preSet, res, nums);
        preSet.pop_back();
        while(i<nums.size()-1 && nums[i+1]==nums[i])//后面的数字如果相等要跳过，不然会导致重复
            i++;
    }
}
vector<vector<int> > subsetsWithDup(vector<int>& nums) {
    sort(nums.begin(), nums.end());
    vector<int> preSet;
    vector<vector<int> > res;
    for (int size = 0; size <= nums.size(); size++)
        backtracking(0, size, preSet, res, nums);
    return res;
}

Leetcode 131. 分割回文串（中等）

给定一个字符串 s，将 s 分割成一些子串，使每个子串都是回文串。

返回 s 所有可能的分割方案。

示例：

1
2
3
4
For example, given s = "aab",  
Return  
[ ["aa","b"],  
["a","a","b"]  ]

题解：
回溯。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
bool isPalindrome(string s, int start, int end){
    while(start<end){
        if(s[start++]!=s[end--])
            return false;
    }
    return true;
}
void partitioning(string s, vector<string> &prePartition, vector<vector<string> > &result){
    if(s.size()==0){
        result.push_back(prePartition);
        return;
    }
    for (int i = 0; i < s.size();i++){
        if(isPalindrome(s,0,i)){
            prePartition.push_back(s.substr(0, i + 1));
            partitioning(s.substr(i + 1, s.size() - (i + 1)), prePartition, result);
            prePartition.pop_back();
        }
    }
}
vector<vector<string>> partition(string s) {
    vector<string> prePartition;
    vector<vector<string> > res;
    partitioning(s, prePartition, res);
    return res;
}

Leetcode 37. 解数独（困难）

通过填充空格来解决数独问题。

一个数独的解法需遵循如下规则：

  1. 数字 1-9 在每一行只能出现一次。
  2. 数字 1-9 在每一列只能出现一次。
  3. 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。

空白格用 ‘.’ 表示。

题解：
回溯。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
int cube(int i, int j){
    return (i / 3) * 3 + j / 3; //0-8
}
bool backtracking(int row, int col, vector<vector<bool> > &rowUsed, vector<vector<bool> > colUsed, vector<vector<bool> > cubeUsed, vector<vector<char> > &board){
    while (row < 9 && board[row][col]!='.'){
        row = col == 8 ? row + 1 : row;
        col = col == 8 ? 0 : col + 1;
    }
    if(row==9)//全部填完
        return true;
    for (int num = 1; num <= 9;num++){
        if(rowUsed[row][num] || colUsed[col][num] || cubeUsed[cube(row,col)][num])
            continue;
        rowUsed[row][num] = true;
        colUsed[col][num] = true;
        cubeUsed[cube(row, col)][num] = true;
        board[row][col] = '0' + num;
        if(backtracking(row,col,rowUsed,colUsed,cubeUsed,board))
            return true;
        board[row][col] = '.';
        rowUsed[row][num] = false;
        colUsed[col][num] = false;
        cubeUsed[cube(row, col)][num] = false;
    }
    return false;
}
void solveSudoku(vector<vector<char>>& board) {
    vector<vector<bool> > rowUsed(9,vector<bool>(10,false));
    vector<vector<bool> > colUsed(9,vector<bool>(10,false));
    vector<vector<bool> > cubeUsed(9,vector<bool>(10,false));
    for (int i = 0; i < 9; i++)
    {
        for (int j = 0; j < 9;j++){
            if(board[i][j]=='.')
                continue;
            int num = board[i][j] - '0';
            rowUsed[i][num] = true;
            colUsed[j][num] = true;
            cubeUsed[cube(i,j)][num] = true;
        }
    }
    backtracking(0, 0, rowUsed, colUsed, cubeUsed, board);
}

N皇后问题

输入n，输出解法的数量。（下一题还需要输出解法）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
void solveNQueen(int n, int row, vector<bool> &diagonal45, vector<bool> &diagonal135, vector<bool> &colUsed, int &res){
    if(row == n){
        res++;
        return;
    }
    for (int col = 0; col < n;col++){
        int idx45 = row + col;
        int idx135 = n - 1 - (row - col);
        if(colUsed[col] || diagonal135[idx135] || diagonal45[idx45])
            continue;
        colUsed[col] = diagonal45[idx45] = diagonal135[idx135] = true;
        solveNQueen(n, row + 1, diagonal45, diagonal135, colUsed, res);
        colUsed[col] = diagonal45[idx45] = diagonal135[idx135] = false;
    }
}

int NQueen(int n){
    int res = 0;
    vector<bool> diagonal45(2 * n - 1, false);
    vector<bool> diagonal135(2 * n - 1, false);
    vector<bool> colUsed(n, false);
    solveNQueen(n, 0, diagonal45, diagonal135, colUsed, res);
    return res;
}

Leetcode 51. N皇后（困难）

给定一个整数 n，返回所有不同的 n 皇后问题的解决方案。

示例：

1
2
3
4
5
6
7
8
9
10
11
12
13
输入: 4  
输出: [  
[".Q..",  // 解法 1  
"...Q",  
"Q...",  
"..Q."],  

["..Q.",  // 解法 2  
"Q...",  
"...Q",  
".Q.."]  
]  
解释: 4 皇后问题存在两个不同的解法。

题解：
回溯。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
void backtracking(int n, int row, vector<bool> &diagonal45, vector<bool> &diagonal135, vector<bool> &colUsed, vector<string> &oneSolution, vector<vector<string> > &res){
    if(row==n){
        res.push_back(oneSolution);
        return;
    }
    for (int col = 0; col < n;col++){
        int idx45 = row + col;
        int idx135 = n - 1 - (row - col);
        if(colUsed[col] || diagonal135[idx135] || diagonal45[idx45])
            continue;
        oneSolution[row][col] = 'Q';
        colUsed[col] = diagonal135[idx135] = diagonal45[idx45] = true;
        backtracking(n, row + 1, diagonal45, diagonal135, colUsed, oneSolution, res);
        colUsed[col] = diagonal135[idx135] = diagonal45[idx45] = false;
        oneSolution[row][col] = '.';
    }
}
vector<vector<string>> solveNQueens(int n) {
    vector<vector<string> > res;
    string tmp = "";
    for (int i = 0; i < n;i++)
        tmp += ".";
    vector<string> oneSolution(n, tmp);
    vector<bool> diagonal45(2*n-1,false);
    vector<bool> diagonal135(2*n-1,false);
    vector<bool> colUsed(n,false);

    backtracking(n, 0, diagonal45, diagonal135, colUsed, oneSolution, res);
    return res;
}

3.6.2 广度优先（BFS）

Leetcode 1091. 二进制矩阵中的最短路径（中等）

可以往8个方向走，0 表示可以经过某个位置，求解从左上角到右下角的最短路径长度。

示例：

1
2
3
4
5
input:   
0 0 0  
1 1 0  
1 1 0  
output: 4 ([0,0],[0,1],[1,2],[2,2])

题解：
队列实现“层序遍历”，bfs。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
int shortestPathBinaryMatrix(vector<vector<int>>& grid) {
    int rows = grid.size();
    int cols = grid[0].size();
    if (rows==0 || cols==0 || grid[0][0]==1 || grid[cols-1][rows-1]==1)
        return -1;

    //从当前点的右边开始逆时针
    int direction[8][2] = { {0, 1}, {1, 1}, {1, 0}, {1, -1}, {0, -1}, {-1, -1}, {-1, 0}, {-1, 1} };
    queue<vector<int> > que;
    que.push({0,0});
    int res = 0;
    while (!que.empty())
    {
        int size = que.size();//这一层有多少节点
        res++;
        while(size-- >0){//把这一层的节点处理完
            vector<int> cur = que.front();
            que.pop();
            if(grid[cur[0]][cur[1]]==1)//已经经过的点
                //由于加入队列的顺序的原因，有些在待处理队列里面的为0的点，会被重复加入队列。
                //如果这里不判断的话，已经更新为1的节点还是会被重复处理
                continue;
            if (cur[0] == rows - 1 && cur[1] == cols - 1)
                return res;

            grid[cur[0]][cur[1]] = 1;//走过的路标记为1
            for(auto d:direction){
                int row = cur[0] + d[0];
                int col = cur[1] + d[1];
                if(row<0 || row>=rows || col<0 || col>=cols || grid[row][col])
                    //超过了上下左右边界 || 不能经过或者已经经过的点
                    continue;
                vector<int> tmp = {row, col};
                que.push(tmp);
            }
        }
    }
    return -1;
}

Leetcode 279. 完全平方数（中等）

给定正整数 n，找到若干个完全平方数（比如 1, 4, 9, 16, …）使得它们的和等于 n。你需要让组成和的完全平方数的个数最少。

示例：

1
2
3
4
5
6
7
given n = 12
return 3
because 12 = 4 + 4 + 4; 

given n = 13
return 2 
because 13 = 4 + 9.

题解：
bfs。可以将每个整数看成图中的一个节点，如果两个整数之差为一个平方数，那么这两个整数所在的节点就有一条边。要求解最小的平方数数量，就是求解从节点 n 到节点 0 的最短路径。本题也可以用动态规划求解，在之前动态规划部分中已经出现。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
int numSquares(int n) {
    queue<int> que;
    que.push(n);  //从n开始或者从1开始都行
    bool marked[n];
    for (int i = 0; i < n;i++)
        marked[i] = 0;//false

    int res = 0;
    while(!que.empty()){
        res++;
        int size = que.size();
        while(size-- > 0){
            int cur = que.front();
            que.pop();
            for(int i = 1; i * i <= n; i++){
                int next = cur - i*i;
                if(next<0)
                    break;
                if(next==0)
                    return res;

                if(marked[next])
                    continue;
                marked[next] = 1;
                que.push(next);
            }
        }
    }
    return 0;
}

Leetcode 127. 单词接龙（中等）

给定两个单词（beginWord 和 endWord）和一个字典，找到从 beginWord 到 endWord 的最短转换序列的长度。转换需遵循如下规则：

  1. 每次转换只能改变一个字母。
  2. 转换过程中的中间单词必须是字典中的单词。

说明:

  • 如果不存在这样的转换序列，返回 0。
  • 所有单词具有相同的长度。
  • 所有单词只由小写字母组成。
  • 字典中不存在重复的单词。
  • 你可以假设 beginWord 和 endWord 是非空的，且二者不相同。

示例1：

1
2
3
4
5
6
7
8
Input:  
beginWord = "hit",  
endWord = "cog",  
wordList = ["hot","dot","dog","lot","log","cog"]  

Output: 5  

Explanation: As one shortest transformation is "hit" -> "hot" -> "dot" -> "dog" -> "cog", return its length 5.

示例2：

1
2
3
4
5
6
7
8
9
Input:  
beginWord = "hit"  
endWord = "cog"  
wordList = ["hot","dot","dog","lot","log"]  

Output: 0  

Explanation: The endWord "cog" is not in wordList, therefore no possible transformation.  
题目描述：找出一条从 beginWord 到 endWord 的最短路径，每次移动规定为改变一个字符，并且改变之后的字符串必须在 wordList 中。

题解：
bfs。官方双向bfs的C++版本。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
int n;
unordered_map<string, vector<string> > umap;

int bfs(queue<pair<string, int> > &curQueue, unordered_map<string, int>& visited, unordered_map<string, int>& anoVisited){
    string curWord = curQueue.front().first;
    int len = curQueue.front().second;
    curQueue.pop();
    for(int i = 0; i < n; ++i){
        string index = curWord.substr(0, i)+"*"+curWord.substr(i+1, n);
        for(string str : umap[index]){
            if(anoVisited[str])
                return len + anoVisited[str]; 
            if(!visited[str]){
                curQueue.push(make_pair(str, len+1));
                visited[str] = len+1;
            }
        }
    }
    return -1;
}

int ladderLength(string beginWord, string endWord, vector<string>& wordList) {
    n = beginWord.size();
    bool flag = false;
    for(string str : wordList){
        for(int i = 0; i < n; ++i){
            string tp = str.substr(0,i)+"*"+str.substr(i+1, n);
            umap[tp].push_back(str);
        }
        if(str == endWord)
            flag = true;
    }
    if(!flag) return 0;//endWord不在wordList里
    
    unordered_map<string, int> beginVisited, endVisited;
    queue<pair<string, int> > begQueue, endQueue;
    begQueue.push(make_pair(beginWord, 1));
    endQueue.push(make_pair(endWord, 1));
    beginVisited[beginWord] = 1;
    endVisited[endWord] = 1;
    while(!begQueue.empty() && !endQueue.empty()){
        int curlen = bfs(begQueue, beginVisited, endVisited);
        if(curlen != -1)
            return curlen;
        curlen = bfs(endQueue, endVisited, beginVisited);
        if(curlen != -1)
            return curlen;
    }
    return 0;
}

3.6.3 深度优先（DFS）

Leetcode 695. 岛屿的最大面积（中等）

查找最大的连通面积。一个 岛屿 是由一些相邻的 1 (代表土地) 构成的组合，这里的「相邻」要求两个 1 必须在水平或者竖直方向上相邻。你可以假设grid的四个边缘都被 0（代表水）包围着。

示例：

1
2
3
4
5
6
7
8
9
[0,0,1,0,0,0,0,1,0,0,0,0,0],  
[0,0,0,0,0,0,0,1,1,1,0,0,0],  
[0,1,1,0,1,0,0,0,0,0,0,0,0],  
[0,1,0,0,1,1,0,0,1,0,1,0,0],  
[0,1,0,0,1,1,0,0,1,1,1,0,0],  
[0,0,0,0,0,0,0,0,0,0,1,0,0],  
[0,0,0,0,0,0,0,1,1,1,0,0,0],  
[0,0,0,0,0,0,0,1,1,0,0,0,0]  
output: 6

题解：

DFS
  1. STL栈实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
int maxAreaOfIsland(vector<vector<int>>& grid) {
    vector<vector<int> > direction = { {0, -1}, {0, 1}, {-1, 0}, {1, 0} };
    int res = 0;
    for (int i = 0; i < grid.size(); i++)
    {
        for (int j = 0; j < grid[0].size();j++){
            int res_ij = 0;
            stack<vector<int> > st;
            vector<int> tmp = {i, j};
            st.push(tmp);
            while (!st.empty())
            {
                int cur_i = st.top()[0];
                int cur_j = st.top()[1];
                st.pop();
                if(cur_i<0 || cur_j<0
                    || cur_i>=grid.size() || cur_j>=grid[0].size()
                    || grid[cur_i][cur_j]!=1 )//这个条件一定要放到最后，要先满足坐标的条件，不然grid会越界
                    continue;
                grid[cur_i][cur_j] = 0;
                res_ij++;
                for (auto dir : direction)
                {
                    int next_i = cur_i + dir[0];
                    int next_j = cur_j + dir[1];
                    vector<int> tmp2 = {next_i, next_j};
                    st.push(tmp2);
                }
            }
            res = max(res, res_ij);
        }
    }
    return res;
}
}
  1. 递归。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
int dfs(vector<vector<int> > &grid,int cur_i, int cur_j){
    if(cur_i<0 || cur_j<0 || cur_i >= grid.size() || cur_j >= grid[0].size() || grid[cur_i][cur_j] != 1)
        return 0;
    grid[cur_i][cur_j] = 0;
    int res = 1;
    int dir_i[] = {1, 0, 0, -1};
    int dir_j[] = {0, 1, -1, 0};
    for (int i = 0; i < 4;i++){
        int next_i = cur_i + dir_i[i];
        int next_j = cur_j + dir_j[i];
        res += dfs(grid, next_i, next_j);
    }
    return res;
}
int maxAreaOfIsland(vector<vector<int>>& grid) {
    int res = 0;
    for (int i = 0; i < grid.size();i++){
        for (int j = 0; j < grid[0].size();j++)
            res = max(res, dfs(grid, i, j));
    }
    return res;
}
BFS也可以

把栈改为队列就行

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
int maxAreaOfIsland(vector<vector<int> > &grid){
    vector<vector<int> > direction = { {0, -1}, {0, 1}, {-1, 0}, {1, 0} };
    int res = 0;
    for (int i = 0; i < grid.size(); i++)
    {
        for (int j = 0; j < grid[0].size();j++){
            int res_ij = 0;
            queue<vector<int> > st;
            vector<int> tmp = {i, j};
            st.push(tmp);
            while (!st.empty())
            {
                int cur_i = st.front()[0];
                int cur_j = st.front()[1];
                st.pop();
                if(cur_i<0 || cur_j<0
                    || cur_i>=grid.size() || cur_j>=grid[0].size()
                    || grid[cur_i][cur_j]!=1 )//这个条件一定要放到最后，要先满足坐标的条件，不然grid会越界
                    continue;
                grid[cur_i][cur_j] = 0;
                res_ij++;
                for (auto dir : direction)
                {
                    int next_i = cur_i + dir[0];
                    int next_j = cur_j + dir[1];
                    vector<int> tmp2 = {next_i, next_j};
                    st.push(tmp2);
                }
            }
            res = max(res, res_ij);
        }
    }
    return res;
}

Leetcode 200. 岛屿数量（中等）

给你一个由 ‘1’（陆地）和 ‘0’（水）组成的的二维网格，请你计算网格中岛屿的数量。

岛屿总是被水包围，并且每座岛屿只能由水平方向或竖直方向上相邻的陆地连接形成。

此外，你可以假设该网格的四条边均被水包围。

示例：

1
2
3
4
5
6
7
8
9
Input:  
[
    ['1','1','0','0','0'],
    ['1','1','0','0','0'],
    ['0','0','1','0','0'],
    ['0','0','0','1','1']
]

Output: 3

题解：
dfs。求矩阵中的连通分量数目。可以将矩阵表示看成一张有向图。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
void dfs(vector<vector<char> > &grid, int i, int j){
    if(i<0 || i>=grid.size() || j<0 || j>=grid[0].size() || grid[i][j]=='0')
        return;
    vector<vector<int> > directions = { {-1, 0}, {1, 0}, {0, -1}, {0, 1} };
    grid[i][j] = '0';
    for(auto d:directions){
        int next_i = i + d[0];
        int next_j = j + d[1];
        dfs(grid, next_i, next_j);
    }
}
int numIslands(vector<vector<char> >& grid) {
    int res = 0;
    for (int i = 0; i < grid.size();i++){
        for (int j = 0; j < grid[0].size();j++){
            if(grid[i][j] != '0'){
                res++;
                dfs(grid, i, j);
            }
        }
    }
    return res;
}

bfs也可以（待补充）

Leetcode 547. 朋友圈（中等）

好友关系可以看成是一个无向图，例如第 0 个人与第 1 个人是好友，那么 M[0][1] 和 M[1][0] 的值都为 1。求朋友圈的个数。

示例：

1
2
3
4
5
6
7
8
9
Input:  
[[1,1,0],  
[1,1,0],  
[0,0,1]]

Output: 2  

已知学生 0 和学生 1 互为朋友，他们在一个朋友圈。
第2个学生自己在一个朋友圈。所以返回 2 。

题解：
dfs。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
void dfs(vector<vector<int> > &nums, int i, vector<bool> &isFriend){
    isFriend[i] = true;
    for (int j = 0; j < nums.size();j++){
        if(!isFriend[j] && nums[i][j]==1){
            dfs(nums, j, isFriend);
        }
    }
}
int findCircleNum(vector<vector<int>>& M) {
    int res = 0;
    vector<bool> isFriend(M.size());
    for (int i = 0; i < M.size(); i++)
    {
        if(!isFriend[i]){
            res++;
            dfs(M, i, isFriend);
        }
    }
    return res;
}

Leetcode 130. 被围绕的区域（中等）

使被 ‘X’ 包围的 ‘O’ 转换为 ‘X’。任何边界上的 ‘O’ 都不会被填充为 ‘X’。

示例：

1
2
3
4
5
6
7
8
9
10
For example,  
X X X X  
X O O X  
X X O X  
X O X X  
After running your function, the board should be:  
X X X X  
X X X X  
X X X X  
X O X X

题解：

  1. dfs方法一。先把和最外侧的’O’相连的’O’用dfs找出来标记成其他，剩下的就是里侧的需要填充的了。填充的时候顺便把不需要填充的’O’换回来
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
void dfs(vector<vector<char> > &board, int i, int j){
    if(i<0 || i>= board.size() || j<0 || j>=board[0].size() || board[i][j] != 'O')
        return;
    board[i][j] = '*';
    vector<vector<int> > directions = { {0,-1},{0,1},{-1,0},{1,0} };
    for(auto d:directions)
        dfs(board, i + d[0], j + d[1]);
    return;
}

void solve(vector<vector<char>>& board) {
    if(board.empty())
        return;
    for (int i = 0; i < board[0].size();i++){
        dfs(board, 0, i);
        dfs(board, board.size() - 1, i);
    }
    for (int i = 0; i < board.size();i++){
        dfs(board, i, 0);
        dfs(board, i, board[0].size() - 1);
    }

    for (int i = 0; i < board.size(); i++){
        for (int j = 0; j < board[0].size(); j++){
            if(board[i][j]=='O')
                board[i][j] = 'X';
            else if (board[i][j]== '*')
                board[i][j] = 'O';
        }
    }
    return;
}
  1. dfs方法二
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
vector<vector<int> > dirs = {{1,0},{-1,0},{0,1},{0,-1}};
void dfs(vector<vector<char>>& board,vector<int> & s,vector<vector<bool> > &marked){
    int x=s[0],y=s[1];
    if(board[x][y]=='X' || marked[x][y])
        return;
    marked[x][y] = true;
    for(auto d:dirs){
        int next_i = x+d[0], next_j = y+d[1];
        vector<int> tmp = {next_i,next_j};
        if((next_i > 0 && next_i < board.size())
        && (next_j > 0 && next_j < board[0].size()))
            dfs(board,tmp,marked);
    }
    return;
}

void solve(vector<vector<char>>& board) {
    if(board.empty())
        return;
    int m = board.size(),n = board[0].size();
    vector<vector<bool> > marked(m,vector<bool>(n, false));
    vector<vector<int> > side;
    for(int i=0;i<n;i++){
        if(board[0][i]=='O'){
            side.push_back({0,i});
            //marked[0][i] = true;
        }
        if(board[m-1][i]=='O'){
            side.push_back({m-1,i});
            //marked[m-1][i] = true;
        }
    }
    for(int i=1;i<m-1;i++){
        if(board[i][0]=='O'){
            side.push_back({i,0});
            //marked[i][0] = true;
        }
        if(board[i][n-1]=='O'){
            side.push_back({i,n-1});
            //marked[i][n-1] = true;
        }
    }

    for(auto s:side){
        dfs(board,s,marked);
    }

    for(int i=0;i<m;i++){
        for(int j=0;j<n;j++){
            if(!marked[i][j] && board[i][j]=='O')
                board[i][j] = 'X';
        }
    }
    return;
}

Leetcode 417. 太平洋大西洋水流问题（中等）

左边和上边是太平洋，右边和下边是大西洋，内部的数字代表海拔，海拔高的地方的水能够流到低的地方，求解水能够流到太平洋和大西洋的所有位置。

示例：

1
2
3
4
5
6
7
8
9
10
11
12
13
Given the following 5x5 matrix:

Pacific ~   ~   ~   ~   ~  
    ~  1   2   2   3  (5) *  
    ~  3   2   3  (4) (4) *  
    ~  2   4  (5)  3   1  *  
    ~ (6) (7)  1   4   5  *  
    ~ (5)  1   1   2   4  *  
    *   *   *   *   * Atlantic

Return:  
[[0, 4], [1, 3], [1, 4], [2, 2], [3, 0], [3, 1], [4, 0]]   
(positions with parentheses in above matrix).

题解：
从边缘逆流dfs，P逆流能到达的地方的标记，A逆流能到达的地方标记，都为1的位置即所求位置

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
void dfs(vector<vector<int> > &matrix, int i, int j, vector<vector<bool> > &canTo){
    if(canTo[i][j])
        return;
    canTo[i][j] = true;
    vector<vector<int> > directions = { {0,1},{1,0},{0,-1},{-1,0} };
    for(auto d:directions){
        int next_i = i + d[0];
        int next_j = j + d[1];
        if(next_i<0 || next_i>=matrix.size() || 
        next_j<0 || next_j>=matrix[0].size() || 
        matrix[next_i][next_j]<matrix[i][j]){//这里i j一定要看清楚！因为i j调了一个小时！
            continue;
        }
        dfs(matrix, next_i, next_j, canTo);
    }
}
vector<vector<int>> pacificAtlantic(vector<vector<int>>& matrix) {
    if(matrix.empty())
        return {};
    int m = matrix.size();
    int n = matrix[0].size();
    vector<vector<bool> > canToAtlatic(m, vector<bool>(n, false));
    vector<vector<bool> > canToPacific(m,vector<bool>(n,false));
    for (int i = 0; i < m; i++){
        dfs(matrix, i, 0, canToPacific);
        dfs(matrix, i, n - 1, canToAtlatic);
    }
    for (int i = 0; i < n; i++){
        dfs(matrix, 0, i, canToPacific);
        dfs(matrix, m - 1, i, canToAtlatic);
    }

    vector<vector<int> > res;
    for (int i = 0; i < m; i++){
        for (int j = 0; j < n;j++){
            if(canToAtlatic[i][j] && canToPacific[i][j]){
                vector<int> tmp = {i, j};
                res.push_back(tmp);
            }
        }
    }
    return res;
}

Leetcode 329. 矩阵中的最长递增路径（困难）

给定一个整数矩阵，找出最长递增路径的长度。

对于每个单元格，你可以往上，下，左，右四个方向移动。 你不能在对角线方向上移动或移动到边界外（即不允许环绕）。

示例 1:

1
2
3
4
5
6
7
8
输入: nums = 
[
  [9,9,4],
  [6,6,8],
  [2,1,1]
] 
输出: 4 
解释: 最长递增路径为 [1, 2, 6, 9]。

示例 2:

1
2
3
4
5
6
7
8
输入: nums = 
[
  [3,4,5],
  [3,2,6],
  [2,2,1]
] 
输出: 4 
解释: 最长递增路径是 [3, 4, 5, 6]。注意不允许在对角线方向上移动。

题解：
有记忆的dfs。
普通dfs会超时，所以加了二位矩阵来记录已经得到的最长序列。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
vector<vector<int> > dirs = { {-1, 0}, {1, 0}, {0, -1}, {0, 1}};

int dfs(vector<vector<int> > &matrix, int i, int j, vector<vector<int> > &memo){
    if(memo[i][j]!=0)
        return memo[i][j];
    memo[i][j] = 1;
    for(auto d:dirs){
        if (i + d[0] >= 0 && i + d[0] < matrix.size() 
            && j + d[1] >= 0 && j + d[1] < matrix[0].size() 
            && matrix[i + d[0]][j + d[1]] > matrix[i][j])
            memo[i][j] = max(memo[i][j], dfs(matrix, i + d[0], j + d[1], memo) + 1);
    }
    return memo[i][j];
}

int longestIncreasingPath(vector<vector<int> >& matrix) {
    if(matrix.empty())
        return 0;
    int m = matrix.size(), n = matrix[0].size();
    vector<vector<int> > memo(m, vector<int>(n, 0));
    int res = 0;
    for (int i = 0; i < m; ++i) {
        for (int j = 0; j < n; ++j) {
            res = max(res, dfs(matrix, i, j, memo));
        }
    }
    return res;
}

时间复杂度：O(mn)
空间复杂度：O(mn)

Leetcode 79. 单词搜索（中等）

给定一个二维网格和一个单词，找出该单词是否存在于网格中。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

示例：

1
2
3
4
5
6
7
8
For example,  
Given board =  
[ ['A','B','C','E'],  
['S','F','C','S'],  
['A','D','E','E']  ]  
word = "ABCCED", -> returns true,  
word = "SEE", -> returns true,  
word = "ABCB", -> returns false.

题解： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
bool dfs(vector<vector<char> > &board, string resWord, vector<vector<bool> > &hasVisited, int i, int j){
    if(resWord.size()==0)
        return true;
    if(i<0 || i>=board.size() || j<0 || j>=board[0].size() || board[i][j]!=resWord[0] || hasVisited[i][j])
        return false;
    hasVisited[i][j] = true;
    vector<vector<int> > directions = { {0, 1}, {1, 0}, {0, -1}, {-1, 0} };
    for(auto d:directions){
        if(dfs(board,resWord.substr(1,resWord.size()-1),hasVisited,i+d[0],j+d[1]))
            return true;
    }
    hasVisited[i][j] = false;

    return false;
}
bool exist(vector<vector<char>>& board, string word) {
    vector<vector<bool> > hasVisited(board.size(),vector<bool>(board[0].size(),false));
    for (int i = 0; i < board.size(); i++)
    {
        for (int j = 0; j < board[0].size();j++){
            if(dfs(board, word, hasVisited, i, j))
                return true;
        }
    }
    return false;
}

Leetcode 257. 二叉树的所有路径（简单）

给定一个二叉树，返回所有从根节点到叶子节点的路径。

示例：

1
2
3
4
5
6
7
8
输入：
     1  
    / \  
   2   3  
    \  
     5 

输出：["1->2->5", "1->3"]

题解： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};

vector<string> res;
void dfs(TreeNode *biTree, string prePath, TreeNode *curNode){
    if(curNode==NULL)
        return;
    string curStr = to_string(curNode->val);
    if (prePath.size() != 0)
        curStr = "->" + curStr;
    prePath = prePath + curStr;
    if (curNode->left == NULL && curNode->right == NULL)
    {
        res.push_back(prePath);
        return;
    }else{
        dfs(biTree, prePath, curNode->left);
        dfs(biTree, prePath, curNode->right);
    }
    prePath = prePath.erase(prePath.size()-curStr.size());
}
vector<string> binaryTreePaths(TreeNode* root) {
    dfs(root, "", root);
    return res;
}

时间复杂度：O(n^2)
空间复杂度：O(n^2)

3.6.4 滑动窗口

滑动窗口算法框架

1
2
3
4
5
6
7
8
9
10
11
12
13
int left = 0, right = 0;

while (right < s.size()) {`
    // 增大窗口
    window.add(s[right]);
    right++;

    while (window needs shrink) {
        // 缩小窗口
        window.remove(s[left]);
        left++;
    }
}

Leetcode 424.替换后的最长重复字符

给你一个仅由大写英文字母组成的字符串，你可以将任意位置上的字符替换成另外的字符，总共可最多替换 k 次。

在执行上述操作后，找到包含重复字母的最长子串的长度。

题解： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int characterReplacement(string s, int k) {
    vector<int> numOfAlpha(26);
    int left = 0, right = 0, res = 0, maxCount = 0;
    while(right<s.size()){
        numOfAlpha[s[right] - 'A']++;
        maxCount = max(maxCount, numOfAlpha[s[right]-'A']);
        if(right-left+1 - maxCount >k){
            numOfAlpha[s[left] - 'A']--;
            left++;
        }
        res = max(res, right - left + 1);
        right++;
    }
    return res;
}

Leetcode 567. 字符串的排列（中等）

给定两个字符串 s1 和 s2，写一个函数来判断 s2 是否包含 s1 的排列。

换句话说，第一个字符串的排列之一是第二个字符串的子串。

示例1:

1
2
3
输入: s1 = "ab" s2 = "eidbaooo"
输出: True
解释: s2 包含 s1 的排列之一 ("ba").

示例2:

1
2
3
输入: s1= "ab" s2 = "eidboaoo"
输出: False

题解：
用一个哈希表保存字母出现的个数，然后使用滑动窗口。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
bool checkInclusion(string s1, string s2) {
    unordered_map<char, int> cmap;
    for(char &c:s1)
        cmap[c]++;
    int idxL = 0, idxR = 0;
    while(idxR < s2.size()){
        char c = s2[idxR++]; //窗口右边增大
        cmap[c]--;
        while(idxL<idxR && cmap[c]<0) //窗口左边减小
            cmap[s2[idxL++]]++;
        if(idxR - idxL == s1.size())
            return true;
    }
    return false;
}

3.6.5 二分查找/折半查找

二分查找框架

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int binarySearch(int[] nums, int target) {
    int left = 0, right = ...;

    while(...) {
        int mid = left + (right - left) / 2;
        if (nums[mid] == target) {
            ...
        } else if (nums[mid] < target) {
            left = ...
        } else if (nums[mid] > target) {
            right = ...
        }
    }
    return ...;
}

有两种计算中值 m 的方式：
m = (l + h) / 2
m = l + (h - l) / 2
l + h 可能出现加法溢出，也就是说加法的结果大于整型能够表示的范围。但是 l 和 h 都为正数，因此 h - l 不会出现加法溢出问题。
所以，最好使用第二种计算法方法。

Leetcode 69. x 的平方根（简单）

实现 int sqrt(int x) 函数。

计算并返回 x 的平方根，其中 x 是非负整数。

由于返回类型是整数，结果只保留整数的部分，小数部分将被舍去。

示例：

1
2
3
4
5
6
Input: 4  
Output: 2  

Input: 8  
Output: 2  
Explanation: The square root of 8 is 2.82842..., and since we want to return an integer, the decimal part will be truncated.

题解：
后面 面试高频 中有返回不是int的实现。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int mySqrt(int x) {
    if(x<=1)
        return x;

    int low = 1, hight = x;
    while(low<=hight){
        int mid = low + (hight - low) / 2;
        if((long)mid * mid==x)
            return mid;
        else if((long)mid * mid>x)
            hight = mid - 1;
        else
            low = mid + 1;
    }
    return hight;
}

时间复杂度：O(logx)
空间复杂度：O(1)

Leetcode 744. 寻找比目标字母大的最小字母

给定一个有序的字符数组 letters 和一个字符 target，要求找出 letters 中大于 target 的最小字符，如果找不到就返回第 1 个字符。

示例：

1
2
3
4
5
6
7
8
Input:  
letters = ["c", "f", "j"]  
target = "d"  
Output: "f"  
Input:  
letters = ["c", "f", "j"]  
target = "k"  
Output: "c"

题解： 

1
2
3
4
5
6
7
8
9
10
11
12
13
char nextGreatestLetter(vector<char>& letters, char target) {
    int n = letters.size();
    int low = 0, hight = n-1;
    while(low<=hight){
        int mid = low + (hight - low) / 2;
        if(letters[mid]<=target)
            low = mid + 1;
        else
            hight = mid - 1;
    }
    char res = low < n ? letters[low] : letters[0];
    return res;
}

时间复杂度：O(logn)
空间复杂度：O(1)

Leetcode 540. 有序数组中的单一元素（中等）

给定一个只包含整数的有序数组，每个元素都会出现两次，唯有一个数只会出现一次，找出这个数。要求以 O(logN) 时间复杂度进行求解，因此不能遍历数组并进行异或操作来求解，这么做的时间复杂度为 O(N)。

示例：

1
2
Input: [1, 1, 2, 3, 3, 4, 4, 8, 8]  
Output: 2

题解：
令 index 为 Single Element 在数组中的位置。在 index 之后，数组中原来存在的成对状态被改变。如果 m 为偶数，并且 m + 1 < index，那么 nums[m] == nums[m + 1]；m + 1 >= index，那么 nums[m] != nums[m + 1]。

从上面的规律可以知道，如果 nums[m] == nums[m + 1]，那么 index 所在的数组位置为 [m + 2, h]，此时令 l = m + 2；如果 nums[m] != nums[m + 1]，那么 index 所在的数组位置为 [l, m]，此时令 h = m。因为 h 的赋值表达式为 h = m，那么循环条件也就只能使用 l < h 这种形式。

1
2
3
4
5
6
7
8
9
10
11
12
13
int singleNonDuplicate(vector<int>& nums) {
    int low = 0, hight = nums.size() - 1;
    while(low<hight){
        int mid = low + (hight - low) / 2;
        if(mid%2==1)  //保证m为偶数
            mid--;
        if(nums[mid] == nums[mid+1])
            low = mid + 2;
        else
            hight = mid;
    }
    return nums[low];
}

时间复杂度：O(logn)
空间复杂度：O(1)

类似的题

Leetcode 136. 只出现一次的数字（简单）

给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。

示例：

1
2
输入: [4,1,2,1,2]
输出: 4

题解：
任何数和其自身做异或运算结果是0，任何数和 0 做异或运算结果仍然是原来的数。所以依次异或就能得到。无序的话也不能用二分来做。

1
2
3
4
5
6
7
int singleNumber(vector<int>& nums) {
    int res = 0;
    for (int num : nums) {
        res ^= num;
    }
    return res;
}

时间复杂度：O(n)
空间复杂度：O(1)

Leetcode 137. 只出现一次的数字 II（中等）

给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现了三次。找出那个只出现了一次的元素。

示例：

1
2
输入: [0,1,0,1,0,1,99]
输出: 99

题解：
哈希表的话空间复杂度为O(n)，但是我们需要空间复杂度为O(1)。具体看题解。

1
2
3
4
5
6
7
8
int singleNumber(vector<int>& nums) {
    int seenOnce = 0, seenTwice = 0;
    for (int num : nums) {
        seenOnce = ~seenTwice & (seenOnce ^ num);
        seenTwice = ~seenOnce & (seenTwice ^ num);
    }
    return seenOnce;
}

时间复杂度：O(n)
空间复杂度：O(1)

Leetcode 278. 第一个错误的版本（简单）

给定一个元素 n 代表有 [1, 2, …, n] 版本，在第 x 位置开始出现错误版本，导致后面的版本都错误。

如果第 m 个版本出错，则表示第一个错误的版本在 [l, m] 之间，令 h = m；否则第一个错误的版本在 [m + 1, h] 之间，令 l = m + 1。因为 h 的赋值表达式为 h = m，因此循环条件为 l < h。

示例：

1
2
3
4
5
6
7
给定 n = 5，并且 version = 4 是第一个错误的版本。

调用 isBadVersion(3) -> false
调用 isBadVersion(5) -> true
调用 isBadVersion(4) -> true

所以，4 是第一个错误的版本。

题解：
二分法。

1
2
3
4
5
6
7
8
9
10
11
int firstBadVersion(int n) {
    int low = 1, hight = n;
    while(low < hight){
        int mid = low + (hight - low) / 2;
        if(isBadVersion(mid))
            hight = mid;
        else
            low = mid + 1;
    }
    return low;
}

时间复杂度：O(logn)
空间复杂度：O(1)

Leetcode 153. 寻找旋转排序数组中的最小值（中等）

假设按照升序排序的数组在预先未知的某个点上进行了旋转。(例如，数组[0,1,2,4,5,6,7]可能变为[4,5,6,7,0,1,2])

示例：

1
2
输入: [3,4,5,1,2]
输出: 1

题解：
二分法。

1
2
3
4
5
6
7
8
9
10
11
int findMin(vector<int>& nums) {
    int low = 0, hight = nums.size() - 1;
    while(low < hight){
        int mid = low + (hight - low) / 2;
        if(nums[mid] <= nums[hight])
            hight = mid;
        else
            low = mid + 1;
    }
    return nums[low];
}

时间复杂度：O(logn)
空间复杂度：O(1)

Leetcode 34. 在排序数组中查找元素的第一个和最后一个位置（中等）

给定一个有序数组 nums 和一个目标 target，要求找到 target 在 nums 中的第一个位置和最后一个位置。

示例：

1
2
3
4
Input: nums = [5,7,7,8,8,10], target = 8  
Output: [3,4]  
Input: nums = [5,7,7,8,8,10], target = 6  
Output: [-1,-1]

题解：
可以用二分查找找出第一个位置和最后一个位置，但是寻找的方法有所不同，需要实现两个二分查找。

我们将寻找 target 最后一个位置，转换成寻找 target+1 第一个位置，再往前移动一个位置。这样我们只需要实现一个二分查找代码即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
int findFirst(vector<int> &nums, int target){
    int low = 0, hight = nums.size() - 1;
    if(target>nums[hight]){
        return -1;
    }
    while(low<hight){
        int mid = low + (hight - low) / 2;
        if(nums[mid]>=target)
            hight = mid;
        else
            low = mid + 1;
    }
    return low;
}
vector<int> searchRange(vector<int>& nums, int target){
    if(nums.empty() || target<nums[0] || target>nums[nums.size()-1])
        return {-1, -1};

    int first = findFirst(nums, target);
    int next = findFirst(nums, target + 1);
    if (first == -1 || nums[first] != target)
        return {-1, -1};

    int last = 0;
    if (next == -1)
        last = nums.size() - 1;
    else
        last = next - 1;
    return {first, last};
}

时间复杂度：O(logn)
空间复杂度：O(1)

Leetcode 315. 计算右侧小于当前元素的个数

给定一个整数数组 nums，按要求返回一个新数组 counts。数组 counts 有该性质： counts[i] 的值是  nums[i] 右侧小于 nums[i] 的元素的数量。

示例：

1
2
3
4
5
6
7
输入：nums = [5,2,6,1]
输出：[2,1,1,0] 
解释：
5 的右侧有 2 个更小的元素 (2 和 1)
2 的右侧仅有 1 个更小的元素 (1)
6 的右侧有 1 个更小的元素 (1)
1 的右侧有 0 个更小的元素

题解：

  1. 归并排序。归并的过程中记录右边比左边小的个数和索引。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
vector<int> indexs; //原始索引
vector<int> ans;  //要求的答案
vector<int> ordered;  //存排好序的临时数组
vector<int> orderedIndex;  //存排好序的临时数组索引

void Merge(vector<int> &nums, int l, int mid, int r){
	int i = l, j = mid + 1, p = l;
	while (i <= mid && j <= r){
		if (nums[i] <= nums[j]){
			ordered[p] = nums[i];
			orderedIndex[p] = indexs[i];
			ans[indexs[i]] += (j - mid - 1);
			i++;
			p++;
		}else{
			ordered[p] = nums[j];
			orderedIndex[p] = indexs[j];
			j++;
			p++;
		}
	}

	while (i <= mid) {
		ordered[p] = nums[i];
		orderedIndex[p] = indexs[i];
		ans[indexs[i]] += (j - mid - 1);
		i++;
		p++;
	}

	while (j <= r){
		ordered[p] = nums[j];
		orderedIndex[p] = indexs[j];
		j++;
		p++;
	}

	for (int k = l; k <= r; k++){
		indexs[k] = orderedIndex[k];
		nums[k] = ordered[k];
	}
}

 void MergeSort(vector<int> &a, int L, int R){
	if (L >= R) 
		return;

	int mid = (L + R) >> 1;
	MergeSort(a, L, mid);
	MergeSort(a, mid + 1, R);
	Merge(a, L, mid, R);
}

vector<int> countSmaller(vector<int> &nums){
	int n = nums.size();
	indexs.resize(n);
	ans.resize(n);
	ordered.resize(n);
	orderedIndex.resize(n);

	for(int i = 0; i < n; ++i)
		indexs[i] = i;

	MergeSort(nums, 0, n - 1);

	return ans;
}

时间复杂度：O(nlogn)
空间复杂度：O(n)

  1. 把数组从后往前的元素依次插入一个初始为空的排序数组，插入的索引即为该元素右侧比它小的元素个数。如： 
    1
    2
    3
    4
    5
    6
    7
    8
    9
    示例 [5,2,6,1]

            排序数组
    step1   [1]         return 0
    step2   [1,6]       return 1
    step3   [1,2,6]     return 1
    step4   [1,2,5,6]   return 2

    所以最后答案为  [2,1,1,0]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
int insertNums(vector<int> &sorted, int num){
	if(sorted.size()==1){
		if(num>sorted[0]){
			sorted.push_back(num);
			return 1;
		}
		else{
			sorted.insert(sorted.begin(),num);
			return 0;
		}
	}

	int l = 0, r = sorted.size()-1;
	int mid = (l + r) / 2;
	while (l <= r)
	{
		if(sorted[mid]<num)
			l = mid + 1;
		else
			r = mid - 1;
		mid = (l+r)/2;
	}
	sorted.insert(sorted.begin()+l, num);
	return l;
}

vector<int> countSmaller(vector<int>& nums) {
	if(nums.empty())
		return {};
	vector<int> sorted;
	vector<int> res(nums.size());
	sorted.push_back(nums[nums.size()-1]);
	for(int i=nums.size()-2;i>=0;i--){
		int idx = insertNums(sorted, nums[i]);
		res[i] = idx;
	}
	return res;
}

时间复杂度：一开始以为是O(nlogn)，后来发现insert是O(n)的复杂度，所以是O(n^2)，就是插入排序的复杂度。但是Leetcode还是过了
空间复杂度：O(n)

3.7 字符串

字符串的统计字符串

给定一个字符串str，返回str的统计字符串。例如“aaabbbbcccd”的统计字符串为“a_3_b_4_c_3_d_1”。

题解： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
string calcuChar(string s){
	char c = s[0];
    int cnt = 1;
	string res = "";
	string cur_s;
	for (int i = 1; i < s.size(); i++){
		if(s[i] == c)
            cnt++;
        else{
			cur_s = c;
			res += (cur_s + "_" + to_string(cnt) + "_");
			c = s[i];
			cnt = 1;
		}
	}
	cur_s = c;
	res += (cur_s + "_" + to_string(cnt));
	return res;
}

暴力匹配

暴力匹配算法框架

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int search(String pat, String txt) {
    int M = pat.length;
    int N = txt.length;
    for (int i = 0; i <= N - M; i++) {
        int j;
        for (j = 0; j < M; j++) {
            if (pat[j] != txt[i+j])
                break;
        }
        // pat 全都匹配了
        if (j == M) return i;
    }
    // txt 中不存在 pat 子串
    return -1;
}

KMP算法

从头到尾彻底理解KMP

Leetcode 28. 实现 strStr()

给定一个 haystack 字符串和一个 needle 字符串，在 haystack 字符串中找出 needle 字符串出现的第一个位置 (从0开始)。如果不存在，则返回  -1。
示例 1:
输入: haystack = “hello”, needle = “ll”
输出: 2
示例 2:
输入: haystack = “aaaaa”, needle = “bba”
输出: -1 

1
（待完善）

BM算法

（待完善）

3.8 并查集（联合-查找算法 Union-find Algorithm）

并查集是一种树型的数据结构，用于处理一些不交集（Disjoint Sets）的合并及查询问题。有一个联合-查找算法（Union-find Algorithm）定义了两个用于此数据结构的操作：

  • Union：将两个子集合并成同一个集合。
    由于支持这两种操作，一个不相交集也常被称为联合-查找数据结构（Union-find Data Structure）或合并-查找集合（Merge-find Set）。
  • Find：找到元素的root结点，每个root结点代表了一个子集。就能确定元素属于哪一个子集。它可以被用来确定两个元素是否属于同一子集。

Leetcode并查集题库

路径压缩

我们在查询过程中只关心根结点是什么，并不关心这棵树的形态(有一些题除外)。因此我们可以在查询操作的时候将访问过的每个点都指向树根，这样的方法叫做路径压缩，单次操作复杂度为𝑂(𝑙𝑜𝑔𝑁)。

代码模版

  • 初始化：把每个元素单独成为一个集合，即自己是自己的父结点
    1
    2
    for(int i=1;i<=n;i++)
        pre[i]=i;
  • 查询（含路径压缩）
    1
    2
    3
    4
    int Find(int x){
        if(x==pre[x]) return x;
        return pre[x]=Find(pre[x]);
    }
  • 合并
    1
    2
    3
    4
    5
    6
    void merge(int x,int y){
        int rootX=Find(x),rootY=Find(y);
        if(rootX!=rootY) pre[rootX]=rootY;
    }
    //主函数内
    merge(a,b);

76. 亲戚

规定：x和y是亲戚，y和z是亲戚，那么x和z也是亲戚。如果x,y是亲戚，那么x的亲戚都是y的亲戚，y的亲戚也都是x的亲戚。
输入格式
第一行：三个整数n,m,p，（n<=5000,m<=5000,p<=5000），分别表示有n个人，m个亲戚关系，询问p对亲戚关系。
以下m行：每行两个数Mi，Mj，1<=Mi，Mj<=N，表示Mi和Mj具有亲戚关系。
接下来p行：每行两个数Pi，Pj，询问Pi和Pj是否具有亲戚关系。
输出格式
P行，每行一个’Yes’或’No’。表示第i个询问的答案为“具有”或“不具有”亲戚关系。

输入

1
2
3
4
5
6
7
8
9
6 5 3
1 2
1 5
3 4
5 2
1 3
1 4
2 3
5 6

输出

1
2
3
Yes
Yes
No

题解（略）

Leetcode每日一题-2020年六月：6月8日

四、面试高频题

4.1 自己实现atoi

这个相当高频，面试遇到过至少2次

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int myAtoi(const string &str){
    string s = str;
    int flag = 1;
    if(str[0]=='-'){
        s = s.substr(1, s.size() - 1);
        flag = -1;
    }
    long res = 0;
    for (int i = 0; i < s.size();i++){
        res = res * 10 + (s[i] - '0');
        if(res>=INT_MAX && flag==1)
            return INT_MAX;
        if(res>INT_MAX && flag==-1)
            return INT_MIN;
    }
    return (int)res * flag;
}

4.2 string模拟数字运算

大数相乘

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
string bigMultiple(string num1, string num2){
    int m = num1.size(), n = num2.size();
    vector<long long> num(m + n - 1, 0); //m位*n位 最小是 m+n-1 位，进位插到前面

    for (int i = 0; i < m;i++){//前面是高位，后面是低位
        int a = num1[i] - '0';
        for (int j = 0; j < n; j++)
        {
            int b = num2[j] - '0';
            num[i + j] += a * b;
        }
    }

    int carry = 0;
    for (int i = num.size() - 1; i >= 0;i--){//前面是高位，后面是低位
        int cur = num[i] + carry;
        num[i] = cur % 10;
        carry = cur / 10;
    }
    while(carry!=0){
        int cur = carry % 10;
        carry /= 10;
        num.insert(num.begin(), cur);
    }

    string res = "";
    for (auto a : num)
    {
        res += to_string(a);
    }
    return res;
}

时间复杂度：O(m*n)
空间复杂度：O(m+n)

大数相加

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
string bigAdd(string &num1, string &num2){
    int i = num1.size() - 1, j = num2.size() - 1;
    int carry = 0;
    string res = "";
    while(i>=0 || j>=0 || carry!=0){
        int n1 = i >= 0 ? num1[i] - '0' : 0;
        int n2 = j >= 0 ? num2[j] - '0' : 0;
        int tmp = n1 + n2 + carry;
        res.push_back('0' + tmp % 10);
        carry = tmp / 10;
        i--;
        j--;
    }
    reverse(res.begin(), res.end());
    return res;
}

大数相减

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
string bigAdd(string &num1, string &num2){
    int i = num1.size() - 1, j = num2.size() - 1;
    int carry = 0;
    string res = "";
    while(i>=0 || j>=0 || carry!=0){
        int n1 = i >= 0 ? num1[i] - '0' : 0;
        int n2 = j >= 0 ? num2[j] - '0' : 0;
        int tmp = n1 + n2 + carry;
        res.push_back('0' + tmp % 10);
        carry = tmp / 10;
        i--;
        j--;
    }
    reverse(res.begin(), res.end());
    return res;
}

string GreaterMinSmaller(string num1, string num2){
    int borrow = 0;
    string res = "";
    int i = num1.size() - 1, j = num2.size() - 1;
    while(i>=0){
        int cur1 = num1[i] - '0' - borrow;
        borrow = 0;
        int cur2 = j >= 0 ? num2[j] - '0' : 0;
        if(cur1 < cur2){
            cur1 += 10;
            borrow = 1;
        }
        res.push_back('0' + (cur1 - cur2));
        i--;
        j--;
    }
    reverse(res.begin(), res.end());
    int not0 = 0;
    while(res[not0]=='0')
        not0++;
    return res.substr(not0);
}

string bigMinis(string &num1, string &num2){
    if(num1 == num2)
        return "0";
    int flag1 = 1, flag2 = 1;
    string s1 = num1, s2 = num2;
    if (num1[0] == '-')
    {
        s1 = s1.substr(1);
        flag1 = -1;
    }
    if (num2[0] == '-')
    {
        s2 = s2.substr(1);
        flag2 = -1;
    }
    if(flag1==-1 && flag2==1)
        return "-" + bigAdd(s1, s2);
    else if (flag1 == 1 && flag2 == -1)
        return bigAdd(s1, s2);
    else if (flag1 == 1 && flag2 == 1)
    {
        bool flag = true;
        if(s1.size()<s2.size()){
            flag = false;
        }else if(s1.size()==s2.size()){
            int idx = 0;
            while(s1[idx]==s2[idx])
                idx++;
            if(s1[idx]>s2[idx])
                flag = true;
            else
                flag = false;
        }
        if(flag)
            return GreaterMinSmaller(s1, s2);
        else
            return "-" + GreaterMinSmaller(s2, s1);
    }
    else if (flag1 == -1 && flag2 == -1)
    {//(-a)-(-b) = -(a-b)
        string res = bigMinis(s1, s2);
        if(res[0]=='-')
            return res.substr(1);
        else
            return "-" + res;
    }
    return "";
}

4.3 位操作

奇偶位交换(unsigned int)

只要把奇数位（从低到高）拿出来左移1位，偶数位拿出来右移1位，再相或。

0xAAAA 的偶数位都为1，0x5555的奇数位都为1，分别相与可以得到奇数位和偶数位。

1
2
3
void swapBit(unsigned int &num){
    num = ((num & 0xAAAA) >> 1) | ((num & 0x5555) << 1);
}

4.4 实现sqrt函数

二分查找

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
float sqrtBiSearch(float n){
    if(n<0)
        return 0.0;
    float eps = 1e-8;
    float left, right;
    if (n > 1){
        left = 0;
        right = n;
    }else{
        left = n;
        right = 1;
    }
    float mid = (left + right) / 2, last;
    while(abs(mid-last) > eps){
        if(mid*mid > n)
            right = mid;
        else
            left = mid;
        last = mid;
        mid = (left + right) / 2;
    }
    return mid;
}

牛顿迭代

x_n+1 = x_n - f(x_n)/f'(x_n)。因为f(x) = x^2 - n，所以f'(x) = 2x，即x = (x + n/x)/2

1
2
3
4
5
6
7
8
9
10
11
float sqrtNewton(float n){
    float eps = 1e-8;
    if(abs(n-0.0) > eps)
        return 0.0;
    float x = n ,last = 0 ;
    while (abs(x-last) > eps){
        last = x ;
        x = (x + n / x) / 2.0 ;
    }
     return x;
}

4.5 抢红包的实现

  1. 每次把需要剩下的保证后面的人至少都有最低金额的钱减掉（比如还剩下10个人，每个人至少1分钱，就需要留下至少0.1元）。把金额*100后用int来做，最后 /100 就能保证 2 位小数。最后一个人为剩下的所有钱。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
vector<float> redBag(const float &money, int cnt){
	int Money = money * 100;
	int minMoney = 1;
	int lastMoney = Money;
	int lastCnt = cnt;
	int maxMoney = lastMoney - lastCnt*minMoney;
	vector<float> res;
	for (int i = 0; i < cnt-1; i++){
		int cur = rand() % maxMoney;
		res.push_back(cur/100.0);
		lastMoney -= cur;
		lastCnt--;
		maxMoney = lastMoney - lastCnt*minMoney;
	}
	res.push_back(lastMoney/100.0);
	return res;
}
  1. 随机生产cnt个整数，这些整数加起来的和为sums，每个人分到的钱就为x/sums * money。((float)(int)(cur * 100) / 100.0)能保证两位小数。最后一个人得到剩下的所有。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
vector<float> redBag(const float &money, int cnt){
	vector<float> res(cnt);
	int sums = 0;
	for (int i = 0; i < cnt; i++){
		res[i] = rand() % cnt;
		sums += res[i];
	}
	float sumM = 0.0;
	for (int i = 0; i < cnt - 1; i++){
		float cur = (res[i] / sums) * money;
		cur = ((float)(int)(cur * 100) / 100.0);
		sumM += cur;
		res[i] = cur;
	}
	res[cnt - 1] = money - sumM;
	return res;
}

Reference